Inégalité de complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Rifilou
- Messages: 5
- Enregistré le: 05 Nov 2020, 21:03
-
 par Rifilou » 05 Nov 2020, 21:04
par Rifilou » 05 Nov 2020, 21:04
Bonjour à tous,
je n'ai pas eu le temps de toucher à cet exercice à ma dernière colle de maths, mais je n'ai aucune idée de comment faire ? Si quelqu'un pouvait me mettre sur la piste, je vous en serai très reconnaissant

Soit z1 et z2 des complexes.
On pose M = max(|z1|;|z2|)
Montrer que pour tout entier naturel n, |z1^n-z2^n|<=n*M^(n-1)*|z1-z2|
-
mathelot
 par mathelot » 05 Nov 2020, 21:17
par mathelot » 05 Nov 2020, 21:17
-
Rifilou
- Messages: 5
- Enregistré le: 05 Nov 2020, 21:03
-
 par Rifilou » 06 Nov 2020, 19:41
par Rifilou » 06 Nov 2020, 19:41
Certes, et merci, mais la résolution de Wikipédia est totalement hors programme. Je pense qu'il y a un moyen plus approprié.
J'ai commencé une récurrence mais mon hérédité n'aboutit pas à ce que je veux, M^n*(1 + n/M) devrait être supérieur ou égal à (n+1)*M^n. Voyez-vous un moyen d'avancer?
Voici ce que j'ai fait:
https://www.dropbox.com/s/0w6aomx7x0vps ... 4.jpg?dl=0

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 06 Nov 2020, 20:52
par Sa Majesté » 06 Nov 2020, 20:52
As-tu essayé
 \sum_{k=0}^{n-1} a^{n-1-k} b^k)
-
Rifilou
- Messages: 5
- Enregistré le: 05 Nov 2020, 21:03
-
 par Rifilou » 06 Nov 2020, 21:11
par Rifilou » 06 Nov 2020, 21:11
Oui, je l’ai fait au début de mon hérédité comme vous pouvez le voir sur l’image sur Dropbox. Mais je bloque plus loin

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 06 Nov 2020, 21:17
par Sa Majesté » 06 Nov 2020, 21:17
OK je n'avais pas vu ton image
Je ne comprends pas pourquoi tu sépares
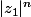
-
Rifilou
- Messages: 5
- Enregistré le: 05 Nov 2020, 21:03
-
 par Rifilou » 06 Nov 2020, 22:12
par Rifilou » 06 Nov 2020, 22:12
Je ne l’ai pas séparé. J’ai arbitrairement choisi que ça allait être la valeur de M. J’ai donc (dans la parenthèse, il faut rajouter le module de z1-z2) (n*M^n-1 + M^n) = (M^n*(n/M + 1). Je me rapproche le plus possible de l’expression que je dois trouver à savoir module(z1-z2)*(n+1)*M^n. Mais je suis bloqué ici


-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 07 Nov 2020, 10:29
par Sa Majesté » 07 Nov 2020, 10:29
Pourquoi est-ce que tu ne majores pas
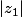
et
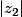
par M dans les expressions de
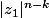
et
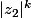
?
-
Rifilou
- Messages: 5
- Enregistré le: 05 Nov 2020, 21:03
-
 par Rifilou » 09 Nov 2020, 22:32
par Rifilou » 09 Nov 2020, 22:32
Finalement j'ai réussi assez simplement:
|z1^n-z2^n|=|(z1-z2)*Somme de 0 à n-1 de (|z1^k *z2^n-k|).
<=|z1-z2|*Somme de 0 à n-1 de (|z1|^k *|z2|^n-k).
<=|z1-z2|*n*|M|^n-1
<=|z1-z2|*n*M^n-1

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 10 Nov 2020, 17:51
par Sa Majesté » 10 Nov 2020, 17:51
Eh oui

Bravo !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités

