Identité de vandermonde généralisée ?

[infernaleur]

Bonsoir !
Je suis bloqué à l'exercice suivant :

Soient:
et

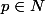
Calculer :


Cette somme me fait penser à l'identité de Van Der Monde, j'ai donc tenté de calculer cette somme en calculant de deux manières (X+1)^n1*(X+1)^n*2...*(X+1)^n_r (comme pour la démonstration classique de l'identité de Van Der Monde) mais je me retrouve rapidement avec des sommes de partout et il est très compliquer d'obtenir une formule.

Je pense peut-être qu'une résolution combinatoire semble plus efficace mais je voudrais savoir si une démonstration algébrique pourrais permettre de calculer cette somme.

Merci beaucoup de votre aide !!!

[Lostounet]

Bonjour Infernaleur,

J'ai un peu réfléchi à ta somme... je pense qu'elle peut s'interpréter en termes de dénombrements (tirer k1 objets dans un sac content n1 boules, k2 dans le second sac de sorte que le total des boules fasse p).

Je pense aussi qu'il est possible d'exprimer comme tu le dis de deux manières ce produit à l'aide des fonctions génératrices discrètes et qu'on peut s'en sortir par identification des coefficients dominants.

Tu veux qu'on essaye?

[infernaleur]

Merci d'avoir pris le temps d'y réfléchir !
Je voudrais bien qu'on essaye ^^
Je vais réessayer pour voir si j'obtiens un résultat et je vous enverrais ce que j'obtiens.

[infernaleur]

Bonjour,
Désoler de répondre aussi tard j'avais beaucoup de travail ...

J'ai un petit souci pour la deuxième manière de calculer (X+1)^n1*...*(X+1)^nr je me retrouve avec énormément de produit de sommes lorsque j'utilise la définition du produit de deux polynômes.

J'ai donc une question car je pense ne pas bien maitriser le produits de sommes.
Pourriez-vous m'expliquer ce que signifie k1+...+kr=p dans une somme (comme dans l'énoncé de l'exercice) , cela m'aiderait surement pour simplifier les calculs.

Merci encore !

[Lostounet]

Après il y a un truc chelou dans la formule: on dispose de r entiers ni (donc n1 à nr) et de r entier ki dans les coefficiens binomiaux. Mais tu sommes sur k1+...+kr=p.

Ce serait pas plutôt k1+...kr=r ?

[infernaleur]

Je n'ai pas de moyen de vérifiée il n'y a pas de corrections, mais je peut le considérer.

[zygomatique]

salut



et tu cherches donc

enfin ce me semble-t-il ...

[infernaleur]

Salut merci zygomatique !
Ma dernière question est comment s'exprime une somme quand l'indice est k1+...+kr=p je n'arrive pas à me représenter cela, pourriez vous m'expliquer svp.
Merci à vous

[zygomatique]

ben ça veut dire qu'on fait la somme sur toutes les possibilités d'avoir S k_i = p sachant que k_i < n_i

[infernaleur]

ok merci