Groupes finis
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
RadarX
- Membre Relatif
- Messages: 333
- Enregistré le: 24 Juil 2005, 19:39
-
par RadarX » 27 Aoû 2006, 19:29
je voudrais reparler (je l'avais evoqué y a longtemps dans ce forum) d'un pb simple. J'ai sous les yeux le resultat suivant:
"Soit G un groupe fini d'ordre n et abelien.
G est simple n est premier." Voyez vous la necessité que G soit
abelien?
Ma preuve est la suivante:
==>
simple. Si
= {
} alors le cas est trivial.
Si G diff de
neutre, soit alors x diff de
. Le sous groupe cyclique est alors egal a G car G est simple; ==>
est cyclique.
Alors si
div
, il existe un sous groupe
(cyclique) d'ordre d (car G cyclique).
Et th de Lagrange ==>
div
; et par simplicité de
,
= {
} ou
==>
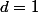
ou
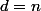
d'ou
premier.
<==
Si n premier, alors
est simple (facile!!?)
Alors, l'utilité de
abelien?
Merci d'avance.
-
RadarX
- Membre Relatif
- Messages: 333
- Enregistré le: 24 Juil 2005, 19:39
-
par RadarX » 27 Aoû 2006, 20:21
RadarX a écrit:Ma preuve est la suivante:
==>
simple. Si
= {
} alors le cas est trivial.
Si G diff de
neutre, soit alors x diff de
. Le sous groupe cyclique est alors egal a G car G est simple; ==>
est cyclique.
Alors si
div
, il existe un sous groupe
(cyclique) d'ordre d (car G cyclique).
Et th de Lagrange ==>
div
; et par simplicité de
,
= {
} ou
==>
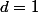
ou
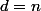
d'ou
premier.
Alors, l'utilité de
abelien?
Si x diff de
. Le sous groupe cyclique
est d'abord distingué car G abelien donc egal a
car
est simple; ==>
est cyclique.
Alors si
div
, il existe un sous groupe
(cyclique) d'ordre
(car G cyclique).
Ai-je bien vu ou pas?
-
kaiser
- Membre Naturel
- Messages: 12
- Enregistré le: 13 Avr 2006, 22:32
-
par kaiser » 27 Aoû 2006, 21:34
Bonsoir RadarX
Effectivement, c'est à ce niveau que l'on se sert du caractère abélien du groupe. En fait, ceci est vrai pour tout sous-groupe de G. En effet, si un groupe est abélien, alors tous ces sous-groupes sont distingués dans G.
Kaiser
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
