Géométrie synthétique : volumes et aires de solides

[srhmrc]

Bonjour, je n'arrive pas à résoudre cet exercice :
" Détermine comment couper une pyramide par un plan parallèle à la base de sorte que le volume du tronc de pyramide ainsi formé soit les 7/8 du volume de la pyramide."
J'ai alors considéré une pyramide de base B et de hauteur H, puis j'ai coupé la pyramide en 2 pour former un tronc de pyramide de hauteur H-x, de petite base b et de grande base B. Par Thalès, et l'énoncé nous dit que . J'ai essayé d'isoler x mais je n'arrive pas à finir le calcul. Ma méthode est-elle correcte?

[Ben314]

Salut,
Je ne comprend pas trop ce que représente tes variables numériques et dans ta formule , mais si c'est sensé être les aires des bases, alors c'est totalement faux et il n'y a besoin d'aucune connaissance pour le voir : Si tu part d'un carré et que tu double la longueur du coté, le nouveau carré contient évidement quatre carrés de départ donc son aire est quatre fois celle de départ (et pas deux fois). 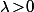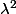Et de façon générale, si on fait une homothétie de rapport , certes, les longueurs sont multipliées par , mais les aires, elles, sont multipliées par , (et les volumes par ).
Bref, si tu part d'un cône (à base quelconque) et que tu fait une homothétie de rapport (centrée au sommet du cône), la hauteur du nouveau cône sera où est la hauteur du cône de départ et le volume du nouveau cône sera où est le volume du cône de départ. Et si tu veut que ce volume soit 1/8 (=1-7/8) de celui de départ, ça veut dire qu'il faut prendre

[srhmrc]

Je m'étais mal exprimée, B est la longueur d'un côté de la grande base, et b la longueur d'un côté de la petite base. Mon raisonnement de départ est-il correct ?

Merci pour l'explication ! Utiliser une homothétie est bien plus simple.

[catamat]

Je m'étais mal exprimée, B est la longueur d'un côté de la grande base, et b la longueur d'un côté de la petite base. Mon raisonnement de départ est-il correct ?

Oui cela peut donner le résultat mais en appliquant la bonne formule (volume d'un tronc de pyramide) car si B est le côté de la base, l'aire de la base est B² de même pour b à remplacer par b².

Ensuite on peut se simplifier la vie en évitant un trop grand nombre d'inconnues.

On garde x mais on peut choisir comme unité de longueur la longueur de la hauteur donc H =1
d'autre part Thalès nous donne b=Bx

L'équation ne contient plus alors que B et x, on peut simplifier par B² et on obtient x^3=1/8 sans surprise...