Bonjour,
je suis en L2 informatique, et j'ai un sujet mathématique que je devrais maîtriser d'ici mi Mars, et je sais pas trop d'ou commencer.
ce que je devrais faire c'est de comprendre le sujet et bien le présenté le jour de ma présentation.
Au fait, on a par exemple un résultat qui est de "0,662271805" qu'on a eu après avoir fait une division entre deux nombres entiers de 3 chiffres, est ce qu'on peut trouver les deux nombres que l'on a divisé au départ uniquement à travers ce résultat ?
jespère que vous aurez des idées à partager avec moi, Merci d'avance
Fraction continues
17 messages
- Page 1 sur 1
par Robic » 17 Fév 2015, 16:59
Bonjour ! Pour ta question, je crois que la réponse est oui grâce à l'unicité de la décomposition en facteurs premiers.
Par exemple avec 0,662271805 tu pars de
et tu décomposes en facteurs premier les deux nombres afin de simplifier la fraction. Ici :
662 271 805 = 5 x 13x 17 x 599 341
et
1 000 000 000 = 2^9 x 5^9
Donc on peut seulement simplifier par 5 :
S'il existait une fraction plus simple, on l'aurait trouvée puisque la décomposition en facteurs premiers est unique.
(Pour le calcul des facteurs premiers, j'ai utilisé un petit programme que j'avais écrit en C il y a quelques années.)
Par exemple avec 0,662271805 tu pars de
662 271 805 = 5 x 13x 17 x 599 341
et
1 000 000 000 = 2^9 x 5^9
Donc on peut seulement simplifier par 5 :
S'il existait une fraction plus simple, on l'aurait trouvée puisque la décomposition en facteurs premiers est unique.
(Pour le calcul des facteurs premiers, j'ai utilisé un petit programme que j'avais écrit en C il y a quelques années.)
par nodjim » 17 Fév 2015, 17:53
Je crois que Doraki a fait la fraction continue (1,1,1,24,1,1,1,1,2).
A confirmer.
A confirmer.
par Robic » 17 Fév 2015, 17:55
Argh, du coup je m'ai planté...
Ah, j'ai compris !
La fraction 653/986 fait en réalité 0,662 271 805 273 833 671 399 594 320 486 815 415 821... Donc ce n'était pas une valeur exacte, du coup je n'ai pas répondu à la bonne question.
Ah, j'ai compris !
La fraction 653/986 fait en réalité 0,662 271 805 273 833 671 399 594 320 486 815 415 821... Donc ce n'était pas une valeur exacte, du coup je n'ai pas répondu à la bonne question.
par sylvainc2 » 17 Fév 2015, 17:58
Oui, à partir de la fraction continue de 662271805 / 10^9 on calcule les réduites et on conserve la plus grande qui tient sur 3 chiffres au numérateur et dénominateur.
unknown007 devrait consuter https://fr.wikipedia.org/wiki/Fraction_continue pour savoir comment faire.
unknown007 devrait consuter https://fr.wikipedia.org/wiki/Fraction_continue pour savoir comment faire.
par unknown007 » 17 Fév 2015, 18:03
Bonjour, Merci pour vos réponses.
@Robic, j'ai déjà pensé à faire ça, mais comme vous l'avez dit, il faudra une fraction plus simple
@Doraki, c'est exactement à ces deux valeurs à quoi je m'attendais, vous avez utiliser quelle méthode ?
@Robic, j'ai déjà pensé à faire ça, mais comme vous l'avez dit, il faudra une fraction plus simple
@Doraki, c'est exactement à ces deux valeurs à quoi je m'attendais, vous avez utiliser quelle méthode ?
par zygomatique » 17 Fév 2015, 18:28
salut
si r est un nombre décimal quelconque de ]0, 1[ l'algorithme est classique (et basé sur la décomposition en fraction continue)
on construit la suite d'entiers a_n par
 \\ r_{n + 1}= r_n - a_n)
et alors
:lol3:
si r est un nombre décimal quelconque de ]0, 1[ l'algorithme est classique (et basé sur la décomposition en fraction continue)
on construit la suite d'entiers a_n par
et alors
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par Robic » 17 Fév 2015, 19:50
Moi qui n'y connais rien en fraction continues, je propose la méthode bourrin :
Lire x (on suppose que x appartient à [0;1[)
eps = 1E-08 (précision meilleure que x)
p := 0 (numérateur final, nécessairement <= q --- mais pas forcément < q (*))
q := 0 (dénominateur final)
distance = 1.0 (distance finale)
pour j = 1 à 999 (dénominateur candidat)
pour i= 1 à j (numérateur candidat)
dist = |x - i/j|
si (dist+eps < distance) alors {distance := dist ; p := i ; q := j}
fin pour i
fin pour j
Afficher p, q
Bon, ça ne fait jamais que de l'ordre du demi-million de calculs... :marteau:
----
(*) Il faut que 0,999 999 donne comme réponse 1/1, d'où le p <= q. De plus il ne faut pas que ça donne 212/212 ou 664/664 sous prétexte qu'avec 212 et 212, la quinzième décimale est plus proche qu'avec 1 et 1, d'où l'utilité du nombre eps.
Lire x (on suppose que x appartient à [0;1[)
eps = 1E-08 (précision meilleure que x)
p := 0 (numérateur final, nécessairement <= q --- mais pas forcément < q (*))
q := 0 (dénominateur final)
distance = 1.0 (distance finale)
pour j = 1 à 999 (dénominateur candidat)
pour i= 1 à j (numérateur candidat)
dist = |x - i/j|
si (dist+eps < distance) alors {distance := dist ; p := i ; q := j}
fin pour i
fin pour j
Afficher p, q
Bon, ça ne fait jamais que de l'ordre du demi-million de calculs... :marteau:
----
(*) Il faut que 0,999 999 donne comme réponse 1/1, d'où le p <= q. De plus il ne faut pas que ça donne 212/212 ou 664/664 sous prétexte qu'avec 212 et 212, la quinzième décimale est plus proche qu'avec 1 et 1, d'où l'utilité du nombre eps.
par sylvainc2 » 01 Mar 2015, 18:54
unknown007 a posé pratiquement la même question sur une autre site sous un autre pseudo, et je lui ai dit comment faire là-bas:
http://forums.futura-sciences.com/mathematiques-superieur/682802-fractions-continues.html
http://forums.futura-sciences.com/mathematiques-superieur/682802-fractions-continues.html
par zygomatique » 01 Mar 2015, 20:50
la seule (au sens de "la plus exacte" du point de vu mathématique) est ce que j'ai dit dans mon précédent post ...
et ça se programme très simplement ....
et ça se programme très simplement ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par Robic » 01 Mar 2015, 21:09
J'avoue que je n'ai pas compris ton algorithme. Manifestement il ne calcule pas le numérateur et le dénominateur de la fraction cherchée, donc que fait-il ? Dans la fraction finale, il y a r, mais il n'y a pas les r1, r2... du coup à quoi ils servent ? Dans les deux suites, que sont a0 et r0 ? Si je choisis r0 = 0,662 271 805 j'obtiens a0 = 1 puis r1 = -0.337 728 195, r2 = 2.662 271 805, r3 = 2,662.271.805 et ça reste constant (vu que 1/rn est alors nul).
Pour m'exercer en Python (langage que je viens de découvrir avant-hier et qui m'a aussitôt séduit : c'est ça qu'il faut enseigner au lycée plutôt qu'Algobox), je viens d'écrire le petit programme correspondant à mon algorithme bourrin :
# Calcul d'une fraction proche d'un nombre entre 0 et 1
r = 0.662271805 ...# le nombre décimal entre 0 et 1
eps = 0.00000000001 ...# précision meilleure que r
p, q = 0.0, 0.0 ...# numérateur et dénominateur
distance = 1.0 ...# distance finale
for j in range (1, 1000) : ...#de 1 à 999
...for i in range (1, j+1) : ...# de 1 à j
......dist = abs(r - i/j)
......if ( dist + eps < distance ) :
.........distance = dist
.........p = i
.........q = j
print (p, "/", q)
Il retourne bien « 653 / 986 » (au bout d'une petite seconde environ).
Je me suis amusé à chercher une fraction proche de 0.14159265358979 (les décimales de Pi) :
- avec un chiffre : le 1/7 bien connu (de sorte que pi ~ 22/7, ce qui donne 2 décimales justes) ;
- avec deux chiffres : 14/99 (de sorte que pi ~ 311/99, ce qui donne 3 décimales justes - presque 4) ;
- avec trois chiffres : 16/113 (de sorte que pi ~ 355/113, ce qui donne 6 décimales justes) ;
- avec quatre chiffres : 16/113 aussi (après quelques dizaines de secondes de calculs) ;
- avec cinq chiffres : 9390/66317 (là il faut quelques dizaines de minutes ! - eh oui, c'est le programme bourrin). Donc pi ~ 208341/66317, avec 10 décimales justes (et c'est bien une fraction irréductible).
Pour m'exercer en Python (langage que je viens de découvrir avant-hier et qui m'a aussitôt séduit : c'est ça qu'il faut enseigner au lycée plutôt qu'Algobox), je viens d'écrire le petit programme correspondant à mon algorithme bourrin :
# Calcul d'une fraction proche d'un nombre entre 0 et 1
r = 0.662271805 ...# le nombre décimal entre 0 et 1
eps = 0.00000000001 ...# précision meilleure que r
p, q = 0.0, 0.0 ...# numérateur et dénominateur
distance = 1.0 ...# distance finale
for j in range (1, 1000) : ...#de 1 à 999
...for i in range (1, j+1) : ...# de 1 à j
......dist = abs(r - i/j)
......if ( dist + eps < distance ) :
.........distance = dist
.........p = i
.........q = j
print (p, "/", q)
Il retourne bien « 653 / 986 » (au bout d'une petite seconde environ).
Je me suis amusé à chercher une fraction proche de 0.14159265358979 (les décimales de Pi) :
- avec un chiffre : le 1/7 bien connu (de sorte que pi ~ 22/7, ce qui donne 2 décimales justes) ;
- avec deux chiffres : 14/99 (de sorte que pi ~ 311/99, ce qui donne 3 décimales justes - presque 4) ;
- avec trois chiffres : 16/113 (de sorte que pi ~ 355/113, ce qui donne 6 décimales justes) ;
- avec quatre chiffres : 16/113 aussi (après quelques dizaines de secondes de calculs) ;
- avec cinq chiffres : 9390/66317 (là il faut quelques dizaines de minutes ! - eh oui, c'est le programme bourrin). Donc pi ~ 208341/66317, avec 10 décimales justes (et c'est bien une fraction irréductible).
par zygomatique » 02 Mar 2015, 13:14
je note E(r) et F(r) les parties entière et fractionnaire du réel r
le principe est le suivant :
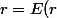 + F(r) = p + s = p + \dfrac 1 {\frac 1 s} = p + \dfrac 1{E(\frac 1 s) + F(\frac 1 s)} = p + \dfrac 1{q + s'})
la première fraction calculée est}1)
la deuxième fraction calculée est
....
que l'on continue jusqu'à la précision voulue en négligeant à chaque fois le terme F(1/s) pour le calcul de la fraction
tout le problème est d'effectuer le calcul intermédiaire de la fraction p/q approximant le réel r
voici l'algorithme ::
lire r
lire e (précision = nombre de décimales)
s = r
a = b = 1
c = 0
p = E(r)
q = 1
Tant que abs (p/q - r)> 10^(-e)
{
d = p
s = 1/F(s)
f = E(s)
p = f*d+a
a=d
q = b*f+c
c= b
b=q
}
afficher r, " = ", p, "/",q
ce programme accepte des entiers et renvoie 2 = 2/1 par exemple
essayer avec pi et e variant de 0 à ? (10 suivant la précision de la machine ou plus : nb de chiffres avec lesquels la machines travaille)
:zen:
le principe est le suivant :
la première fraction calculée est
la deuxième fraction calculée est
....
que l'on continue jusqu'à la précision voulue en négligeant à chaque fois le terme F(1/s) pour le calcul de la fraction
tout le problème est d'effectuer le calcul intermédiaire de la fraction p/q approximant le réel r
voici l'algorithme ::
lire r
lire e (précision = nombre de décimales)
s = r
a = b = 1
c = 0
p = E(r)
q = 1
Tant que abs (p/q - r)> 10^(-e)
{
d = p
s = 1/F(s)
f = E(s)
p = f*d+a
a=d
q = b*f+c
c= b
b=q
}
afficher r, " = ", p, "/",q
ce programme accepte des entiers et renvoie 2 = 2/1 par exemple
essayer avec pi et e variant de 0 à ? (10 suivant la précision de la machine ou plus : nb de chiffres avec lesquels la machines travaille)
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par Robic » 02 Mar 2015, 20:09
Merci pour ta réponse ! Voilà le programme correspondant en Python :
----------------------------------------
# Calcul d'une fraction à partir de fractions continues
# (algorithme fournit par Zygomatique)
#r = 3.141592653589793238462643383279
r = 0.662271805 # le nombre décimal
e = 10 # précision (nombre de décimales demandées)
s = r
a, b = 1, 1
c = 0
p = int( r )
q = 1
print ("r =", p, "/", q, "=", p/q)
#while (abs(p/q - r) > 10**(-e)) :
n = 0
while (n < 15) :
... n += 1
... d = p
... s = 1/(s-int(s))
... f = int(s)
... p = f * d + a
... a = d
... q = b * f+c
... c = b
... b = q
... print ("r =", p, "/", q, "=", p/q)
----------------------------------------
(J'ai mis en commentaire la boucle qui arrête à la précision demandée pour voir ce qui se passe itération par itération.)
On obtient :
r = 0 / 1 = 0.0
r = 1 / 1 = 1.0
r = 1 / 2 = 0.5
r = 2 / 3 = 0.6666666666666666
r = 49 / 74 = 0.6621621621621622
r = 51 / 77 = 0.6623376623376623
r = 100 / 151 = 0.6622516556291391
r = 151 / 228 = 0.6622807017543859
r = 251 / 379 = 0.662269129287599
r = 653 / 986 = 0.6622718052738337
r = 2452266 / 3702809 = 0.6622718049999339
r = 2452919 / 3703795 = 0.6622718050000067
r = 24528537 / 37036964 = 0.6622718049999995
r = 26981456 / 40740759 = 0.6622718050000002
r = 132454361 / 200000000 = 0.662271805
r = 159435817 / 240740759 = 0.662271805
Pour Pi :
r = 3 / 1 = 3.0
r = 22 / 7 = 3.142857142857143
r = 333 / 106 = 3.141509433962264
r = 355 / 113 = 3.1415929203539825
r = 103993 / 33102 = 3.1415926530119025
r = 104348 / 33215 = 3.141592653921421
r = 208341 / 66317 = 3.1415926534674368
r = 312689 / 99532 = 3.1415926536189365
r = 833719 / 265381 = 3.141592653581078
r = 1146408 / 364913 = 3.141592653591404
r = 4272943 / 1360120 = 3.141592653589389
r = 5419351 / 1725033 = 3.1415926535898153
r = 80143857 / 25510582 = 3.1415926535897927
r = 245850922 / 78256779 = 3.141592653589793
r = 817696623 / 260280919 = 3.141592653589793
r = 19052873251 / 6064717916 = 3.141592653589793
----------------------------------------
# Calcul d'une fraction à partir de fractions continues
# (algorithme fournit par Zygomatique)
#r = 3.141592653589793238462643383279
r = 0.662271805 # le nombre décimal
e = 10 # précision (nombre de décimales demandées)
s = r
a, b = 1, 1
c = 0
p = int( r )
q = 1
print ("r =", p, "/", q, "=", p/q)
#while (abs(p/q - r) > 10**(-e)) :
n = 0
while (n < 15) :
... n += 1
... d = p
... s = 1/(s-int(s))
... f = int(s)
... p = f * d + a
... a = d
... q = b * f+c
... c = b
... b = q
... print ("r =", p, "/", q, "=", p/q)
----------------------------------------
(J'ai mis en commentaire la boucle qui arrête à la précision demandée pour voir ce qui se passe itération par itération.)
On obtient :
r = 0 / 1 = 0.0
r = 1 / 1 = 1.0
r = 1 / 2 = 0.5
r = 2 / 3 = 0.6666666666666666
r = 49 / 74 = 0.6621621621621622
r = 51 / 77 = 0.6623376623376623
r = 100 / 151 = 0.6622516556291391
r = 151 / 228 = 0.6622807017543859
r = 251 / 379 = 0.662269129287599
r = 653 / 986 = 0.6622718052738337
r = 2452266 / 3702809 = 0.6622718049999339
r = 2452919 / 3703795 = 0.6622718050000067
r = 24528537 / 37036964 = 0.6622718049999995
r = 26981456 / 40740759 = 0.6622718050000002
r = 132454361 / 200000000 = 0.662271805
r = 159435817 / 240740759 = 0.662271805
Pour Pi :
r = 3 / 1 = 3.0
r = 22 / 7 = 3.142857142857143
r = 333 / 106 = 3.141509433962264
r = 355 / 113 = 3.1415929203539825
r = 103993 / 33102 = 3.1415926530119025
r = 104348 / 33215 = 3.141592653921421
r = 208341 / 66317 = 3.1415926534674368
r = 312689 / 99532 = 3.1415926536189365
r = 833719 / 265381 = 3.141592653581078
r = 1146408 / 364913 = 3.141592653591404
r = 4272943 / 1360120 = 3.141592653589389
r = 5419351 / 1725033 = 3.1415926535898153
r = 80143857 / 25510582 = 3.1415926535897927
r = 245850922 / 78256779 = 3.141592653589793
r = 817696623 / 260280919 = 3.141592653589793
r = 19052873251 / 6064717916 = 3.141592653589793
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :