Formule des 3 niveaux

[titine]

Bonjour.
Je viens de trouver cette formule dans un bouquin.
Elle dit que si P est un polynôme de degré 2 :
= (b-a)/6 * (P(a)+P(b)+4P((a+b)/2)

J'ai réussi sans problème à vérifier cette formule mais je me demande comment elle a été trouvé. Corespond elle à une propriété géométrique.

Merci.

[fahr451]

bonsoir

pour moi la formule des n niveaux est autre chose et la formule des deux niveaux un cas particulier qui permet de montrer que si f " >= 0 alors f est convexe

je ne connaissais pas cette formule des trois niveaux

[mathelot]

ça , à vue de nez, c'est le calcul de l'intégrale par la méthode des trapèzes
qui doit être exacte pour les polynomes de degré inférieur à 3.

[nuage]

Salut,
il s'agit de la méthode de Simpson. Voila ce qu'en dit wikipédia.
Par parenthèse il me semble que la majoration de l'erreur donnée dans l'artcle est pessimiste.
Je vais vérifier.
A+

[fahr451]

simpson d'après wikipédia ne convergerait pas ... puisque quand n tend vers l 'infini l erreur trouvée aussi;

elle est en fait pour f de classe C 4 en (b-a)^5 ll f^(4)llinfinie /(2880n^4)

en 1/n^4 donc

[yos]

Je viens de trouver cette formule dans un bouquin.
Elle dit que si P est un polynôme de degré 2 :
= (b-a)/6 * (P(a)+P(b)+4P((a+b)/2)

J'ai réussi sans problème à vérifier cette formule mais je me demande comment elle a été trouvé. Corespond elle à une propriété géométrique.

Bonjour.
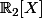
Les applications et sont des formes linéaires sur . Les trois dernières forment une base de l'espace vectoriel , et la première s'exprime dans cette base avec les coefs indiqués.
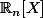
La généralisation à est immédiate. Voilà pour la "géométrie".
Pour trouver les coefs dans ce cas comme dans le cas général, il faut voir cette base comme la base duale d'une base de .

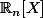
[nuage]

simpson d'après wikipédia ne convergerait pas ... puisque quand n tend vers l 'infini l erreur trouvée aussi;

elle est en fait pour f de classe C 4 en (b-a)^5 ll f^(4)llinfinie /(2880n^4)

en 1/n^4 donc

Dans Wikipédia le terme est en .
Mais c'est le au dénominateur qui, me chagrinais. Ce que tu donne est plus conforme à mes souvenirs. Que je n'ai toujours pas vérifiés.

[fahr451]

cf nuage ah vi y a h^5 ds leur formule mais bon zauraient pu écrire 1/n^4 pour que ça saute aux yeux

1/2880 oui oui ; je peux te redonner la (une) fonction auxiliaire à considérer si tu veux le redémontrer

[titine]

Merci de vos réponses.