Bonsoir,
Pour une colle prochaine sur les DL, j'ai gentiment pondu la fonction suivante (je ne suis pas un colleur si sadique que ça :we:) :
x -> exp(1-ch(x)) - cos(x)
Ma question (de pure curiosité et qui n'a rien à voir avec les DL) concerne cette horrible fonction car j'ai essayé (en vain et vu qu'elle intervient plus loin au dénominateur d'un autre DL à faire - là, ça devient sadique alors je ne le mets pas) de trouver ses zéros...
En fait, je montre sans problème qu'elle ne s'annule en un voisinage de 0, qu'en 0, et aussi une infinité de fois par un simple encadrement... mais j'aimerais montrer qu'elle s'annule "autant de fois" que le cosinus, en fait... Disons que la régularité de ch et de exp fait que c'est très clair sur Maple, et une fois qu'on s'éloigne de 0, très rapidement cette fonction colle à -cos et en devient une courbe asymptotique en l'infini...
Quelqu'un aurait-il une idée pour montrer que cette fonction ne s'annule pas n'importe comment, n'importe quand (genre sin(1/x)), mais en suivant les variation de cos ? Ca paraît très évident et intuitif quand on la voit, mais à montrer, c'est une autre histoire (notamment parce que pour étudier les variations via la dérivée, il faut se lever de bonne heure !!).
Merci de vos contributions.
Cordialement, DedenK.
Fonction moche à partir d'éléments simples...
4 messages
- Page 1 sur 1
salut,
assez curieusement, cette fonction est très facile à étudier
mais avec encadrement et images réciproques d'intervalles.
heuristique:
Quand x tend vers l'infini (f est paire)
=exp(1-ch(x))) est "presque" à support compact.
est "presque" à support compact.
pour < 10^{-3})
comme on le voit avec))
lim g = 0 , g est décroissante, positive, tend vers zéro quand x tend vers très rapidement.
très rapidement.
La courbe de=-\cos(x)=cos(x-\pi)) est une sinusoïde habituelle.
est une sinusoïde habituelle.
On découpe le domaine de définition de f en la réunion de trois familles
dénombrables d'intervalles. On travaille avec la relation d'ordre.
a) Une réunion dénombrable d'intervalle où le cos est positive ou nulle.
Sur cette réunion, f(x) ne s'annule pas,est positive.
b) Une réunion dénombrable d'intervalle où le cos est négative,
inférieure strictement à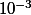
Sur cette réunion, f(x) ne s'annule pas, est négative.
Le complémentaire est une famille dénombrable d'intervalles
la dérivée de f est:
=exp(1-ch(x))(-sh(x)) + sin(x))
on pose s=ch(x)
)sh(x)| \leq \frac{es}{exp(s)})
tend rapidement vers zéro quand s tend vers l'infini.
|f'(x) -sin(x)| tend vers zéro quand x tend vers
Sur les intervalles où cos() est proche de 0 en valeur absolue,
inférieure à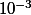 ,
,
|sin(x)| est proche de 1
f ' ne s'annule donc pas sur ces intervalles.
Avec le TVI, on conclue:
sur ces derniers intervalles, f est strictement monotone et s'annule donc une fois et une seule.
Conclusion: la courbe de f suit donc la courbe sinusoide de)
assez curieusement, cette fonction est très facile à étudier
mais avec encadrement et images réciproques d'intervalles.
heuristique:
Quand x tend vers l'infini (f est paire)
pour
comme on le voit avec
lim g = 0 , g est décroissante, positive, tend vers zéro quand x tend vers
La courbe de
On découpe le domaine de définition de f en la réunion de trois familles
dénombrables d'intervalles. On travaille avec la relation d'ordre.
a) Une réunion dénombrable d'intervalle où le cos est positive ou nulle.
Sur cette réunion, f(x) ne s'annule pas,est positive.
b) Une réunion dénombrable d'intervalle où le cos est négative,
inférieure strictement à
Sur cette réunion, f(x) ne s'annule pas, est négative.
Le complémentaire est une famille dénombrable d'intervalles
la dérivée de f est:
on pose s=ch(x)
tend rapidement vers zéro quand s tend vers l'infini.
|f'(x) -sin(x)| tend vers zéro quand x tend vers
Sur les intervalles où cos() est proche de 0 en valeur absolue,
inférieure à
|sin(x)| est proche de 1
f ' ne s'annule donc pas sur ces intervalles.
Avec le TVI, on conclue:
sur ces derniers intervalles, f est strictement monotone et s'annule donc une fois et une seule.
Conclusion: la courbe de f suit donc la courbe sinusoide de
Merci...
Bonjour et merci.
Effectivement, c'est drôle mais hier soir, en allant me coucher, j'ai pensé à un truc du genre... sauf que je m'apprêtais à utiliser la convexité sur le petit intervalle pour majorer la dérivée...
Je regarderai ça de près cet après-midi, mais ça m'a l'air de bien marcher.
Encore merci.
Cordialement, DedenK.
Effectivement, c'est drôle mais hier soir, en allant me coucher, j'ai pensé à un truc du genre... sauf que je m'apprêtais à utiliser la convexité sur le petit intervalle pour majorer la dérivée...
Je regarderai ça de près cet après-midi, mais ça m'a l'air de bien marcher.
Encore merci.
Cordialement, DedenK.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
