Fonction lipschitzienne

[Johnny001]

bonjour à tous et à toutes les matheux !!

Connaissez vous une démonstration qui montrerait que les fonctions x² et racine(x) ne sont pas lipschitzienne ?

Merci d'avance

[Nightmare]

elles ne sont pas uc sur le domaine de définition.

[Johnny001]

elles ne sont pas uc?

Voilà c'est sa que je voulais savoir, tu pourrais m'expliquer en quelques mots ce que signifie :"leur dérivée n'est pas bornée".

Merci d'avance ;)

[B_J]

Salut ;
pour
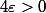
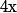
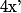
il faut determiner un reel tel que pour tout réel , il existe deux reels et verifiant
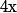
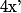
quelconque , il nous faut determiner un reel independant de et deux reels et dependant eventuellement de tels que :

choisissons et
on a donc et
, ce qui prouve que n'est pas uniformement continue sur

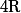
[Nightmare]

uc = uniformément continues.

une fonction est lipschitzienne si et ssi f' est bornée, ie si et seulement si il existe M tel que pour tout x |f'(x)|< M

La dérivée de x->x² est x->2x qui n'est clairement pas bornée (puisqu'elle tend vers +oo et -oo respectivement en +oo et -oo)

[B_J]

rq: lipschitzienne uniformement continue

[bruce.ml]

uc = uniformément continues.

une fonction est lipschitzienne si et ssi f' est bornée, ie si et seulement si il existe M tel que pour tout x |f'(x)|< M

Attention ! ceci est faux.
Une fonction DERIVABLE est lipschitzienne si et ssi f' est bornée :langue:

[Nightmare]

Bien sûr, cependant si je parle de f', c'est bien que f est dérivable. Ne chipotons pas pour rien.

[bruce.ml]

oui mais non, ce n'est pas pour rien. Ca s'appelle la rigueur, et ça permet de ne pas se tromper dans bien des cas !

[SimonB]

C'est pas pour rien, hein, à force d'oublier cette hypothèse, j'ai déjà vu quelqu'un en colle dériver la fonction racine carrée sur R+ en sup...

[quinto]

Si la racine carrée était lipschitzienne, alors le taux de variation serait borné au voisinage de 0, ce qui n'est pas le cas.