Fonction LIPSCHITZIENNE

[ilhtennis]

Bonsoir à tous , pour résoudre un exo , ça m'aiderait bcp si ma fonction était Lipschitzienne, j'ai une fonction continue bornée dans R , est ce que je peux dire qu'elle est lipschitzienne?
svp dites oui hihi
Merci

[Finrod]

Non, pas de chance.

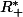
Tu prends Cos(1/x) continue bornée sur . Au voisinage de 0 elle n'est pas lipschitzienne.

En effet f(x)-f(y) peut valoir jusqu'à 2 alors que x-y peut être pris aussi petit qu'on veux.

Donne plus de détails, on pourra surement t'aider.

[ilhtennis]

Merci pour votre réponse , j'ai un exercice théorique
Soit X1,...Xn une suite de variables aléatoires réelles avec Xn tend vers c en probas, et g une fonction R->R continue et bornée , montrer que g(Xn) tend vers g(c) en probas ( c constante)

[Finrod]

arg j'avais écris un truc mais un raccourci clavier me l'a flingué.

Bon pour résumer, avec la def de continuité tu as un |g(x)-g(c)|>e qui implique |x-c|> f et tu peux trouver f qui tend vers 0 en fonction de e.

[ilhtennis]

donc elle est uniformément continue , c'est ça ?

[Nightmare]

Sur tout compact oui, mais sur R tout entier pas forcément. Par exemple sin(x²) est continue et bornée mais n'est pas uniformément continue sur R.

[ilhtennis]

Merci vraiment , j'avais un peu oubli" ces choses là

[klaus2010]

arg j'avais écris un truc mais un raccourci clavier me l'a flingué.

Bon pour résumer, avec la def de continuité tu as un |g(x)-g(c)|>e qui implique |x-c|> f et tu peux trouver f qui tend vers 0 en fonction de e.

plutôt |x-c|< f implique |g(x)-g(c)|<e..

[girdav]

plutôt |x-c|< f implique |g(x)-g(c)|<e..

C'est la contraposée, non?

[ilhtennis]

oui c'est la contraposée