Fonction indicatrice d'euler

par **gauss2** » 17 Aoû 2006, 18:34

bonjour a tout le monde je suis nouveau...
voila je mamuse un peu avec la fonction d'euler mais je n'arrive pas a demontrée certaines propriétées....pourriez vous m'aider svp.

Proposition I.6 : (Théorème de la fonction d'Euler) " n N*, " a ÎN*, tels que n et a soient premiers entre eux :
aj(n) = 1 (mod n)
Démonstration :

par **tize** » 17 Aoû 2006, 18:47

Dans Z/nZ, a premier avec n signifie que a est inversible (utilise la relation de Bézout). D'autre part le groupe des elements inversible de Z/nZ :

comptent exactemtent

element (il y a équivalence entre :est inversible et est premier avec n) où

est l'indicatrice d'euler. Dans un group l'ordre de tout element divise l'ordre du groupe c'est le cas pour l'ordre de "a" (l'ordre de a divise

) dans

donc

par **gauss2** » 17 Aoû 2006, 19:24

tu as été rapide..... j'ai oubliée de préciser que je suis en 1ere année de licence de ce fait je ne connais pas trop la theorie des groupes et meme si je connais un peu Z/nZ je ne comprend pas cette phrase:"Dans un group l'ordre de tout element divise l'ordre du groupe c'est le cas pour l'ordre de "a" "
mais j'ai tout de meme noter ta demonstration...j'en ai plein d'autre de propriétées sur cette fonction que je ve démontré...

par **gauss2** » 17 Aoû 2006, 19:34

en voila une autre: quelque soit n appartenant a N*, n superieur a 3 : phi(n) est pair.

c'est facile de le demontrée pour n premier mais pour le reste c'est plus ardue :briques:

par **tize** » 17 Aoû 2006, 19:35

Si

appartient à un groupe fini

, l'ordre de

est le plus petit entier positif

tel que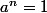

(si la loi du groupe est notée multiplicativement

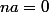si c'est additivement). Il y a un théorème (de Cauchy je crois) qui dit que l'ordre d'un élément

divise toujours l'ordre (le cardinal) du groupe

. Si

est l'ordre du groupe

alors l'ordre de

est un entier qui divise

, il existe donc

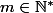tel que :

d'où

.

En espérant avoir été plus clair. N'hésite pas à demander si ça n'est pas le cas.

par **tize** » 17 Aoû 2006, 19:41

Si

est la décomposition en facteur premier de

tu peux trouver explicitement la valeur de

en fonction des

et des

.
Commence par trouver

pour

premier.
Ensuite exprime

.
Et enfin exprime

pour

et

premiers entre eux.
Après tu peux conclure facilement

par **RadarX** » 17 Aoû 2006, 19:44

je pense que le thm dont parle Gauss2 est clairement celui ci:

si x est premier avec n >0 alors x^phi(n) = 1 mod n.
En precisant que phi est la fonction indicatrice d'euler et que phi(n) est le nombre de nombres premiers avec n et inferieurs a n ou bien encore le cardinal (l'ordre) de (Z/nZ)* (les inversibles de l'anneau Z/nZ).

La preuve du thm?
-savoir d'abord que (Z/nZ)* est un groupe multiplicatif (et non additif comme Z/nZ)
- ensuite que l'ordre cad le card de (Z/nZ)* vaut justement phi(n).
Donc si x premier avec n, alors x + nZ (Z/nZ)* et donc
(x+nZ)^phi(n) = 1+ nZ qui l'element neutre de (Z/nZ)*. Car dans un groupe fini d'ordre, x^n = e qq soit x G.
Or (x+nZ)^phi(n) = 1+ nZ x^phi(n) + nZ = 1 + nZ
x^phi(n) = 1 mod n.

Voila, j'espere avoir ete clair; mais c'est vrai qu'il faut un peu de temps pour se familiariser avec des notions pour qq de 1é annee.

par **gauss2** » 17 Aoû 2006, 19:48

sa me parrait tres claire je me rends compte que se n'été pas si difficile... celle ci me parais pas mal non plus:: " quelque soit n appartenant a N*, n superieur 3 : phi(n) superieur à (n . ln (2)) / (ln(n) + ln(2))...

je te rapelle qu'il ny a aucune contrainte c'est seulement pour le plaisir en fait je souhaite etudier cette fonction en entier.

par **tize** » 17 Aoû 2006, 20:03

Une méthode consiste il me semble à d'abord trouver explicitement la valeur de

en fonction des

et des

comme je te l'ai suggéré dans mon dernier message puis faire quelques petites manipulations du résultat.

par **gauss2** » 17 Aoû 2006, 21:45

on a : phi(p)=p-1 pour p premier mais apres je ne sait pas comment trouver phi(p^a)...pouriez vous m'aider...

par **gauss2** » 17 Aoû 2006, 21:51

j'ai encore une autre propriété interresante :
lim n phi(n) = inf

elle parait evidente mais elle n'est pas facile a demontré je ne sais meme pas par ou commencé lol.... :help: :hum:

par **RadarX** » 17 Aoû 2006, 22:00

gauss2 a écrit:on a : phi(p)=p-1 pour p premier mais apres je ne sait pas comment trouver phi(p^a)...pouriez vous m'aider...

phi(p^a) est le nb de nb premiers avec p^a et inferieurs a p^a. Or les nb premiers avec p^a sont exactement les nb prmiers avec p, cad tous les nb inferieus a p^a et non multiples de p (car n'oublions pas que p est premier).
Decomptons les alors:
1,..., p-1,P, p+1,...,2P, 2p+1 ........3P, ......... P^a = p^(a-1).P
De 1 à p il y en a P-1, de P+1 à 2p il y en a p-1..... de p^(a-1) à p^(a-1).p, aussi p-1. Ce qui fait au total (p-1) p^(a-1).
Vla! Ne disposant pas d'un bon editeur de texte, c'est un peu fouilli comme demo.
J'espere avoir fait l'affaire.

par **gauss2** » 17 Aoû 2006, 22:17

ok je crois avoir compris il me desormais exprimer phi(mn) avec m et n premies entre???????? je sais juste que phi(mn)=phi(n)phi(m) c'est une propriété que j'ai deja demontrée mais cea ne m'avance pas... :briques: :stupid_in

par **RadarX** » 17 Aoû 2006, 22:17

gauss2 a écrit:j'ai encore une autre propriété interresante :
lim n phi(n) = inf

elle parait evidente mais elle n'est pas facile a demontré je ne sais meme pas par ou commencé lol.... :help: :hum:

Moi je pense que tu brules des etapes la Illustrissime GAUSS2. Il serait peut etre mieux que tu attaques la theorie des groupes meme legerement d'abord, en bifurquant assez tot sur le cas Z, son arthmetique et enfin sur Z/nZ. Par cette methode tu ne manqueras pas de rencontrer de maniere progressive la fonction phi et ses qq propietes.

T'en penses quoi?

par **gauss2** » 17 Aoû 2006, 22:26

en fait je me déja pencher sur cette théorie j'ai appris ce que c'etait z/nz et osi j'ai jeté un oeil sur certaine propriétées qui pourrais me servir mais il est vraie que je suis peut etre trop curieux en plus plus j'apprend des choses plus il y en a snif c'est pour cela que je m'interesse a cette fonction elle m'empeche de me perdre dans l'immensité des mathématique.... :cry:

par **gauss2** » 17 Aoû 2006, 22:44

je viens de trouver un site trés bien fait sur la theorie des groupes il est tres complet et tres clair je vous donne ladresse et j'invite tous les passionées de math pour qui cette theorie parait obscur d'aller y faire un tour....

http://www.mathou.org

par **RadarX** » 17 Aoû 2006, 23:17

http://www.mathou.org
Il ne marche pas ce site: inaccessible!

par **gauss2** » 17 Aoû 2006, 23:35

essai ceci:

http://mmathou.club.fr/index.html

Fonction indicatrice d'euler

fonction indicatrice d'euler

Qui est en ligne