Fonction gamma et théorème de convegence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mysterion
- Membre Relatif
- Messages: 117
- Enregistré le: 30 Jan 2012, 14:15
-
 par Mysterion » 02 Juil 2013, 13:45
par Mysterion » 02 Juil 2013, 13:45
Salut,
J'aimerais montrer que pour tout t>0
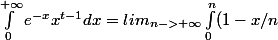^n x^{t-1} dx)
Bon, je reconnais rapidement la la suite de fonctions qui tend vers exp(-x), mais alors une première question :
Qu'elle théorème de convergence utiliser pour pouvoir intervertir intégrale et limite ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 02 Juil 2013, 18:24
par cuati » 02 Juil 2013, 18:24
Bonsoir,
tu peux utiliser le théorème de convergence dominée :
=\left(1-\frac{x}{n}\right)^n\mathbb{1}_{[0,n]}(x))
.
Il suffit de montrer l'inégalité :
\leq e^{-x})
-
Mysterion
- Membre Relatif
- Messages: 117
- Enregistré le: 30 Jan 2012, 14:15
-
 par Mysterion » 02 Juil 2013, 19:06
par Mysterion » 02 Juil 2013, 19:06
cuati a écrit:Bonsoir,
tu peux utiliser le théorème de convergence dominée :
=\left(1-\frac{x}{n}\right)^n\mathbb{1}_{[0,n]}(x))
.
Il suffit de montrer l'inégalité :
\leq e^{-x})
merci pour ta réponse. Et pour être honnête en posant la question je pensais au th. de cv dominée. Mais la difficulté est de montrer la domination. Je n'y arrive pas, essayé mais en vain. Est-ce que tu a l'astuce ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 02 Juil 2013, 19:16
par cuati » 02 Juil 2013, 19:16
De l'inégalité classique :
\leq u)
(concavité de ln valable pour u>-1), on trouve exactement ce que tu recherches.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
.