Fonction contractante

[Supernova]

Bonsoir;

Aidez-moi svp à mq cette application est contractante parce que, franchement, je n'ai aucune idée pour commencer.
L'appli est F: EE
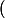
f où g est définie par g:]0,1[--> qui à chaque t-->1/6 ( f() -f() )
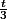
E={ f £ C(]0,1[ , ) / t-->tf(t) est bornée}
(E,N) est de Banach (je l'ai démontré) avec N: t sup|t f(t)|, t ]0,1[

Merci d'avance

[DamX]

Bonsoir;

Aidez-moi svp à mq cette application est contractante parce que, franchement, je n'ai aucune idée pour commencer.
L'appli est F: E--->E
f---->g où g est définie par g:]0,1[-->IR qui à chaque t-->1/6 [f(t/2) -f(t/3)]
E={ f £ C(]0,1[ , IR) / t-->f(t) est bornée}
(E,N) est de Banach (je l'ai démontré) avec N: t--> sup|t f(t)|, t £ ]0,1[

Merci d'avance

Hello,

j'ai fait ça vite fait j'espère ne pas me tromper :

déjà tu peux voir que F linéaire, ainsi pour montrer que F est contractante il suffit de montrer que N(F(f)) < N(f) (car N(F(f)-F(g)) = N(F(f-g)) ).

puis pour tout t, que peux tu dire de |tF(f)(t)| ? ne peux tu pas le comparer à N(f) ?

Damien

[Supernova]

Hello,

j'ai fait ça vite fait j'espère ne pas me tromper :

déjà tu peux voir que F linéaire, ainsi pour montrer que F est contractante il suffit de montrer que N(F(f)) < N(f) (car N(F(f)-F(g)) = N(F(f-g)) ).

puis pour tout t, que peux tu dire de |tF(f)(t)| ? ne peux tu pas le comparer à N(f) ?

Damien

|t F(f(t))| < 5/6 N(f) ??

[DamX]

|t F(f(t))| < 5/6 N(f) ??

Et oui ! et c'est valable pour tout t, donc N(F(f)) < ?
et voilà c'est fini !

[Supernova]

Merci Damien tu m'as sauvé la vie ^^