Fonction avec du arcos(x)et du th(x)

[singular]

Bonsoir, dans un exercice j'ai la fonction suivante que j'ai commencé d'étudier:
f(x)=arcos(th(x))+arctan(sh(x))

J' ai d'abord dit que f était définie sur [-1;1] et dérivable sur ]-1;1[
J'ai rappelé la formule 1-(th(x))²= (a)

je calule la dérivée et j'obtiens f'(x)=- + =0 en utilisant (a)

On me demande ensuite d'en déduire une exression simplifiée de f mais là je bloque , pourriez vous s'il vous plait me donner des pistes....merci.

[Doraki]

Bnosoir, tu connais beaucoup de fonctions compliquées dont la dérivée est constante égale à 0 ?

[singular]

oui HOULà excusez moi oui en effet on a f(x)=cte=f(0)=Pi/2 ciao!

[mathelot]

Bjr,




d'où la formule "symétrique", agréable à mémoriser:




Les liens entre trigo classique et trigo hyperbolique
sont assez mystérieux:

le nombre n'intervient jamais dans les fonctions hyperboliques
(sh,ch,th)

en hyperbolique, on travaille avec la fonction

en trigo classique, le nombre est omniprésent

on travaille avec la fonction

sans doute, ça correspond à deux mondes antithétiques, obtenus
avec les coordonnées de

est-ce que les physiciens pourraient concevoir un monde physique sans le nombre où partout la variable réelle serait remplacée par l'imaginaire pur ?
ou alors concevoir notre monde selon la variable , l'anti-matière selon la variable et unifier tout cela selon la variable
Là, ça devient délirant... :zen:

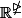
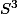
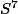
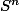
assez curieusement la sphère unité de , noté est l'une des rares sphères à posséder une structure de groupe de lie et la sphère unité de a aussi de bonnes propriétés, et pas les autres sphères pour . Est-ce que ceçi explique cela ?