Fitting d'un triangle équilatéral sur un nuage de points

[sylvain231]

Bonjour à tous,
j'ai un nuage de points et je souhaiterais fitter le meilleur triangle équilatéral passant le plus près de ces points.
Merci de m'aider.
Cordialement

[sylvain231]

je précise que mes points sont les contours d'une forme fermée.

[GaBuZoMeu]

Bonjour,
Comment as-tu obtenu ton nuage de points ?

[sylvain231]

par une technique de deep-learning appelée "segmentation d'instances". Elle permet de trouver automatiquement le contour d'objets

[GaBuZoMeu]

À vrai dire, ta réponse ne m'éclaire pas beaucoup. Un exemple d'image de tel nuage de points me serait plus utile pour voir ce qu'il en est.
Un truc bateau : un triangle équilatéral dans le plan dépend de quatre paramètres (sa taille, les coordonnées de son centre de gravité, son orientation) ; on peut ajuster ces paramètres pour minimiser la somme, sur tous les points du nuage, des carrés du produit des distances aux trois droites supports des côtés.

[sylvain231]

les contours sont variés mais ils forment des formes fermées et chaque point est à 1 pixel maximum de ses voisins

[GaBuZoMeu]

Peux-tu poster une image ? Par ailleurs je t'ai indiqué un procédé, sans garantie que ça donne un résultat satisfaisant.

[sylvain231]

bonsoir,
en fait c'est pour un programme de mesures automatiques de spores de champignons, j'ai géré tous les cas sauf les spores triangulaires. En effet dans ce cas particulier la longueur de la spore n'est pas le segment le plus long entre deux points de contour (qui serait dans ce cas un côté du triangle) mais la hauteur.
Il faut donc dans un premier temps modéliser la spore par un triangle dans tous les cas puis calculer l'IoU (intersection over union) pour voir si cette spore est "à peu près" triangulaire ou non. Puis gérer les deux cas séparément.
J'extrais les contours des spores par deep-learning et traitement d'images.
Je te joins une image de spores non triangulaires :

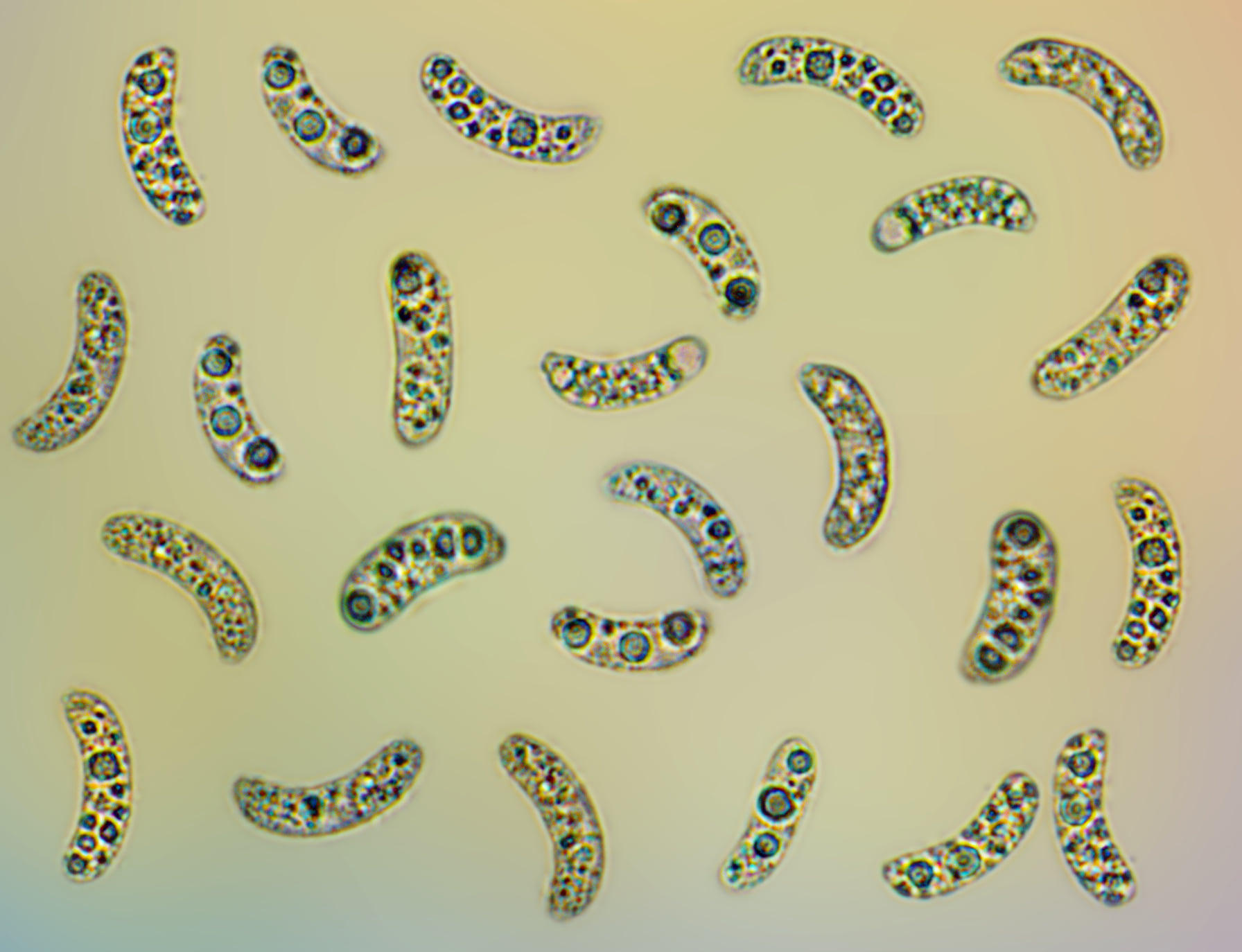
et une de spores quasi-triangulaires :

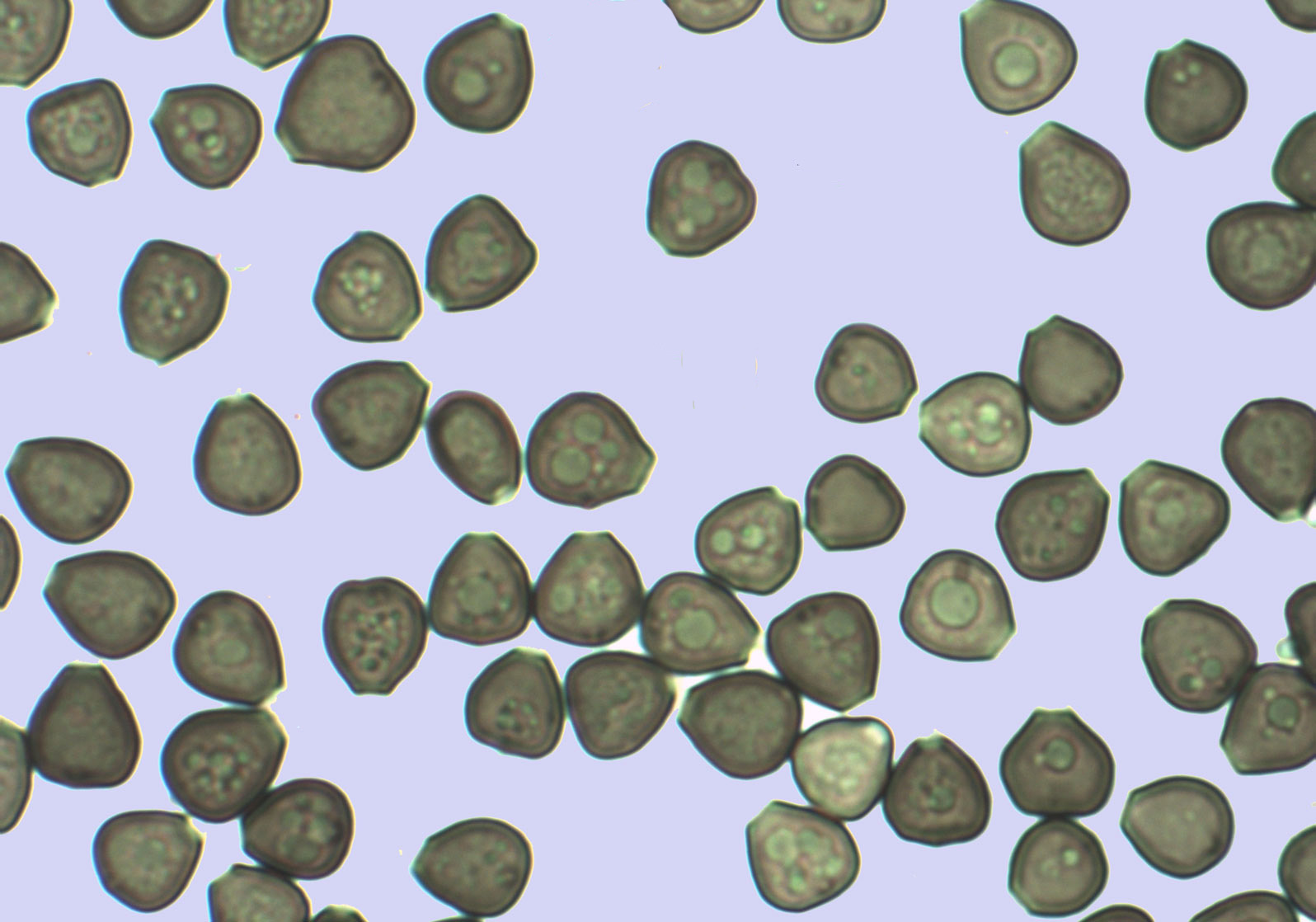
voilà sinon je suis bien incapable de faire une régression triangulaire.

[sylvain231]

aurais-tu des lectures sur les régressions à me conseiller et si tu me fais un pseudo-code déjà prêt aurais-tu l'amabilité de bien me l'expliquer que je puisse moi-même faire des régressions dans d'autres cas futurs qui pourraient se présenter STP ?