Factoriser X^(2n+1)+1
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
allmess
- Membre Naturel
- Messages: 70
- Enregistré le: 12 Sep 2014, 18:46
-
 par allmess » 29 Jan 2015, 18:46
par allmess » 29 Jan 2015, 18:46
Bonjour,
Tout est dans le titre... Quelqu'un pourrais il me donner une piste?
Je n'arrive pas à voir la forme des racines de -1..
Merci :)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Jan 2015, 19:02
par chan79 » 29 Jan 2015, 19:02
allmess a écrit:Bonjour,
Tout est dans le titre... Quelqu'un pourrais il me donner une piste?
Je n'arrive pas à voir la forme des racines de -1..
Merci

Salut
Divise ton polynôme par (x+1)
(x^{2n}-x^{2n-1}+\ ...\ -x+1))
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 29 Jan 2015, 19:04
par nodjim » 29 Jan 2015, 19:04
Vérifie que ça marche avec (x+1)(x^2n-x^(2n-1)+x^(2n-2)-....+1)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Jan 2015, 19:08
par zygomatique » 29 Jan 2015, 19:08
salut
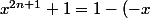^{2n +1} = (1 - (-x)) \sum_0^{2n} (-x)^k)
somme géométrique .... de raison -x ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 29 Jan 2015, 19:35
par wserdx » 29 Jan 2015, 19:35
J'ai l'impression que ce que tu cherches est

Les racines 2n+1 èmes sont donc
i\pi}{2n+1}}, k = 0, \ldots, 2n)
La factorisation sur

est donc
i\pi}{2n+1}})
Pour une factorisation sur

, tu regroupes les racines conjuguées deux à deux
soit
\prod_{k=0}^{n-1}x^2-\cos(\frac{(2k+1)\pi}{2n+1})x+1)
-
allmess
- Membre Naturel
- Messages: 70
- Enregistré le: 12 Sep 2014, 18:46
-
 par allmess » 29 Jan 2015, 19:43
par allmess » 29 Jan 2015, 19:43
Super, merci beaucoup à vous tous, j'ai mes réponses! :we:
Bonne soirée!!

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Jan 2015, 19:55
par zygomatique » 29 Jan 2015, 19:55
malheureusement

:mur: un énoncé clair et précis fut le bienvenu plutôt qu'un titre trompeur ....
résoudre l'équation

conduisait immédiatement
t} = e^{i\pi})
à k2pi près bien sur ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
