Extensions/groupes cycliques

[Lostounet]

Bonsoir,

J'aurais besoin de quelques rappels (ou des indications pour les autres) pour une des questions suivantes. Toute aide (sur n'importe laquelle) est la bienvenue.

1) Si on a une extension Q(√3,√5) et qu'on veut en donner une base sur Q, quel est le moyen le plus simple de justifier que c'est (1, √3, √5, √15) ?
Par exemple on peut scinder avec la base téléscopique en [Q[√3,√5): Q(√3)] x [Q[√3]:Q].
Sinon j'ai pensé à écrire Q(√3, √5) = Q(√3+√5) puis trouver le poly minimal de deg 4 (mais ensuite il faut justifier que les 4 nombres sont "Q"linéairement indépendants)

2) Si on a une extension intermédiaire , si on prend , est-ce qu'on peut comparer [K(a):K] et [L(a):L] ?

3) Par ailleurs il y a un exo que j'ai pas compris: Expliciter un isomorphisme de groupe commutatif

Trouver une CNS sur a et b pour que soit un groupe cyclique

[Ben314]

1) Ben... tout les moyens que tu cite sont bon, modulo qu'il y a un argument qui est pas au bon endroit :
- Déjà, pour montrer que (1, √3, √5, √15) est une base, il suffit de montrer que c'est générateur (un peu chiant, pas bien compliqué) et que c'est Q-libre (idem).
- De passer par une extension intermédiaire Q(√3,√5)=Q(√3)(√5) est plus malin : Q(√3) est trivialement de degré 2 sur Q vu que √3 n'est pas dans Q mais est racine de X²-3 qui est dans Q[X]. Ensuite, Q(√3)(√5) est au plus de degré 2 sur Q(√3) vu que √5 est racine de X²-5 qui est dans Q(√3)[X]. Et pour montrer que c'est effectivement de degré 2 et pas 1, il suffit de montrer que √5 n'est pas dans Q(√3) ce qui n'est pas sorcier.
- Enfin, de chercher le polynôme minimal de a=√3+√5, c'est pas con, mais si tu le cherche en écrivant les puissances de a à l'aide de (1, √3, √5, √15) et en résolvant un système linéaire, ça demande effectivement à montrer que la famille est libre et ça devient sans grand intérêt vu que tu aura déjà quasiment fait tout le boulot (c.f. la deuxième méthode où on voit qu'il suffit de montrer que √5 n'est pas dans Q(√3) pour conclure). Par contre, sans présupposer que la famille en question est libre, tu obtient quand même un polynôme annulateur de a (mais tu n'a pas la preuve qu'il est minimal) est il est possible qu'en utilisant un critère classique tu arrive à montrer l'irréductibilité du polynôme sur Q.

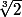
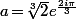
2) Le polynôme minimal P de a sur K (donc P dans K[X]) est évidement un polynôme annulateur de a sur L (vu que K[X]cL[X]) donc [L(a):L][K(a):a] et je pense pas qu'on puisse dire mieux (i.e. que le premier divise le second) : si K=Q, L=Q[] et alors [K(a):K]=3 et [L(a):L]=2.

3) On peut soit le faire "plus où moins à la main" en cherchant un représentant par classe puis en cherchant la structure de groupe de cet ensemble de représentant, soit en étudiant correctement l'équation x+iy=(4+8i)(s+it) (on cherche une c.n.s. sur x et y pour qu'il existe s,t tels que...) de façon à trouver un morphisme de Z[i] dans un certain Z/mZ x Z/nZ dont miraculeusement le noyau serait précisément (4+8i)Z[i].

Idem pour l'autre question, sauf que là, "à la main", c'est mal barré....

P.S. Pour toi, "cyclique", ça veut juste dire monogène ou bien ça veut dire monogène ET fini ?

[Lostounet]

Salut Ben tout d'abord merci,

Pour moi je pensais que cyclique voulait dire monogène et fini.

1
3) On peut soit le faire "plus où moins à la main" en cherchant un représentant par classe puis en cherchant la structure de groupe de cet ensemble de représentant, soit en étudiant correctement l'équation x+iy=(4+8i)(s+it) (on cherche une c.n.s. sur x et y pour qu'il existe s,t tels que...) de façon à trouver un morphisme de Z[i] dans un certain Z/mZ x Z/nZ dont miraculeusement le noyau serait précisément (4+8i)Z[i].

Si on étudie à la main cette équation,
x + iy = (4 + 8i)(s + it)

Elle équivaut à:
x + iy = 4s + 4it + 8is - 8t
(x - 4s + 8t) + i(y - 4t -8s) = 0

x = 4s + 8t
y = 4t + 8s

Donc:
s = 1/12 (2 y - x) et t = 1/12 (2 x - y)

Cela laisse supposer que 2y - x doit être multiple de 12 non?

[Ben314]

- Déjà, c'est pas 12 mais 20
- Ensuite, c'est quand même plus simple de dire directement que
Donc le bilan, c'est que
Et évidement, ça donne envie de considérer le morphisme

dont le noyau est justement .

Sauf que... ça fourni pas un isomorphisme.
Pourquoi ? et comment y remédier ?

P.S. Sinon, "cyclique", ça dépend des auteurs.
Par exemple dans l'article de Wiki, ils prennent juste "monogène" comme définition.

[Lostounet]

Hm...
Est-ce lié au lemme chinois? Ou pas..?

[Ben314]

J'sais pas trop ce que c'est le "lemme chinois", mais de toute façon, là c'est lié à... rien de théorique... (à la limite on peut y voire un eu de théorie des systèmes linéaires si on y tient vraiment...)

[Lostounet]

J'sais pas trop ce que c'est le "lemme chinois", mais de toute façon, là c'est lié à... rien de théorique... (à la limite on peut y voire un eu de théorie des systèmes linéaires si on y tient vraiment...)

Si je prends un couple (x ; y) et que je fais une division (euclidienne) par 20, la réduction modulo 20 doit donner quelque chose comme:
x + 2y = 20q + r
- 2x + 1y = 20q' + r'

Pour que tu dises que ça marche pas il y a plusieurs possibilités: le morphisme n'est pas bien défini ?

[Ben314]

Je vois vraiment pas où il pourrait y avoir de problème de définition dans ça :

Un élément de , il s'écrit pas de façon unique sous la forme avec ?
Existe t'il des entier qu'on ne peut pas multiplier par 2 ? qu'on ne peut pas ajouter/soustraire ? dont on ne peut pas prendre la classe modulo 20 ?
Et concernant le fait que c'est un morphisme de groupes (additifs), c'est complètement immédiat vu que tout ce qui apparait là dedans est trivialement -linéaire (et si tu as des doutes, ben écrit le...)
Enfin, le fait que le noyau, c'est exactement , ben c'est ce qu'on a montré précédemment avec la série d'équivalence.

Donc tout ça, ça prouve que . . . mais ça ne prouve pas que . . .

Remarque : Avec que ça, on peut quand même déduire qu'il existe un isomorphisme tel que celui demandé par l'énoncé, sauf qu'on ne sait pas exactement combien valent et et qu'on ne le connait pas explicitement (alors qu'on doit le donner).

[Lostounet]

Salut,

C'est un morphisme de groupes mais je ne suis pas encore absolument certain qu'il soit bijectif.
Donc toi tu dis que ce morphisme nous permet de déduire l'existence d'un isomorphisme? (Sans l'avoir encore explicité)

[Ben314]

C'est un morphisme de groupes mais je ne suis pas encore absolument certain qu'il soit bijectif.

Le fait que ce morphisme là ne soit pas bijectif, ben c'est complètement évident : on vient de dire que son noyau c'était je_sais_pas_quoi qui est pas du tout réduit à {0}.

[Lostounet]

On doit donc changer de morphisme ou bien quotienter par quelque chose ou le modifier?

[Ben314]

On doit donc changer de morphisme ou bien quotienter par quelque chose ou le modifier?

a ton avis...

[Lostounet]

En fait on a construit un morphisme de Z[i] dans Z/20Z ^2.
Ce qu'il faut faire c'est quotienter par (4+8i)Z[i]?

Pour le moment on a m=n=20 non?

[Ben314]

Ben oui, il faut évidement quotienter par le noyau du morphisme et c'est la raison même pour laquelle depuis le début on cherchais un morphisme dont le noyau soit (4+8i)Z[i] : pour quotienter...

Donc le morphisme se quotiente en un morphisme de de Z[i]/(4+8i)Z[i] dans (Z/20Z)².
Et ce nouveau morphisme est . . .

[Lostounet]

Ben oui, il faut évidement quotienter par le noyau du morphisme et c'est la raison même pour laquelle depuis le début on cherchais un morphisme dont le noyau soit (4+8i)Z[i] : pour quotienter...

Donc le morphisme se quotiente en un morphisme de de Z[i]/(4+8i)Z[i] dans (Z/20Z)².
Et ce nouveau morphisme est . . .

Il me semble qu'on doit réduire " modulo (4+8i)(s+it)" dès le départ ?
Par le théorème de factorisation des morphismes de groupe...

[Ben314]

Il me semble qu'on doit réduire " modulo (4+8i)(s+it)" dès le départ ?

????
Et sinon, oui, c'est effectivement un des théorème "de base" concernant les morphisme de groupes qu'on utilise (plus ou moins le premier théorème d'isomorphisme).
Et ce qu'on sait, c'est que l'application est . . .

[Lostounet]

Et ce qu'on sait, c'est que l'application est . . .

Un isomorphisme qui renvoie Z[i]/(4+8i)Z[i] sur l'image de l'application phi ?

[Ben314]

Oui.
Donc le problème, c'est uniquement de regarder si est surjective ou pas vu que si elle l'est ben c'est fini et on a notre isomorphisme. (et si elle l'est pas, on a un isomorphisme sur un sous groupe de (Z/20Z)², sauf qu'on sait pas lequel c'est, ni à quel Z/nZ x Z/mZ il est isomorphe donc c'est pas trop "explicite")

[Lostounet]

Je ne suis pas parvenu à montrer qu'elle est surjective...vu que moi-même je ne suis pas convaincu qu'elle l'est.
Je sais pas si je m'y prends bien mais j'ai considéré un couple de classes modulo Z/20Z (u,v).
Je dois montrer que je peux toujours trouver des antécédents (x;y) tels que l'on ait les relations entre ces 4 inconnues (système diophantien).

[Ben314]

Je te laisse chercher : d'une façon ou d'une autre (*) il faut absolument que tu arrive à faire un truc pareil, à savoir montrer qu'une telle application est ou n'est pas surjective, voire même, si elle ne l'est pas, déterminer quel est l'image de qui est un sous groupe de (Z/20Z)².

Une fois que tu aura la réponse (à savoir qu'elle n'est pas surjective), cherche quel argument un peu théorique mais rapide qui permettait de se douter qu'il y avait un problème.
Et ensuite, cherche comment "rectifier le tir", c'est à dire comment obtenir un truc surjectif (si on réfléchi "dans le bon sens", c'est assez évident)

(*) A la limite, je te signale quand même que (Z/20Z)² est trivialement engendré par les classes de (1,0) et de (0,1) donc il suffit de résoudre les équations et pour conclure.