Expression de la somme d'une série bien connue
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aviateur
 par aviateur » 01 Juil 2017, 23:54
par aviateur » 01 Juil 2017, 23:54
Bonjour
Il est bien connu que
} {n} \in \R .)
Mais une expression simple de

est-elle connue?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 02 Juil 2017, 01:08
par Lostounet » 02 Juil 2017, 01:08
aviateur a écrit:Bonjour
Il est bien connu que
} {n} \in \R .)
Mais une expression simple de

est-elle connue?
Salut Aviateur,
Il existe une identité:
}{n}} = \frac{\pi - x}{2})
qui se prouve par Riemann-Lebesgue et en se ramenant à l'intégrale du sinus cardinal sur R.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
aviateur
 par aviateur » 02 Juil 2017, 09:14
par aviateur » 02 Juil 2017, 09:14
Merci Lostounet.
En fait mon but initial n'était pas le calcul de S mais par un moyen détourné
j'avais trouvé que
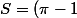/2)
sans tout justifier.
Effectivement la série de Fourier de
/2)
donne bien
/2=\sum_{n\geq 1} \sin(n x)/n)
(égalité dans

et par le théorème de Dirichlet l'égalité est ponctuelle au moins pour la valeur qui m'intéresse.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
est-elle connue?