Exercice "Pot pourri polynômes"
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Déc 2010, 18:51
par benekire2 » 20 Déc 2010, 18:51
Bonsoir à tous !
J'ai trouvé un exercice sur les polynômes composé de plusieurs questions, indépendantes, et presque a toutes les questions je plante ( il y en a une que je connais donc je me suis rappelé de la preuve).
1. Trouver tout les

tels que
=Q(P))
2. Soit

de degré n>0 tel que 1 ne soit pas une racine de P et vérifiant
}{P(1)} \le \frac{deg P}{2})
Montrer que P admet une racine de module supérieur à 1.
3. Calculer
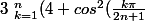))
et

4. Soit

Soit k une racine de P de multiplicité strictement supérieure à la moitié du degré de P, montrer que k est une racine rationnelle.
5. Soit n un entier naturel strictement supérieur à 2. Montrer qu'il n'existe pas de polynômes P,Q,R à coefficients complexes et non tous trois proportionnels tels que

La seule et unique question que j'ai réussie a faire est la 4 , pour le reste :triste: et pourtant je suis certain que certaines questions sont loin d'être insurmontables !!
Merci :lol3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 19:00
par Nightmare » 20 Déc 2010, 19:00
Salut,
avant de réfléchir aux autres, le 4 on l'a déjà traité ensemble [url="http://www.maths-forum.com/polynomes-107062_3.php"]ici[/url] et, je n'ai pas relu le topic, mais il me semble que tu étais arrivé à trouver une preuve.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Déc 2010, 19:04
par benekire2 » 20 Déc 2010, 19:04
Nightmare a écrit:Salut,
avant de réfléchir aux autres, le 4 on l'a déjà traité ensemble [url="http://www.maths-forum.com/polynomes-107062_3.php"]ici[/url] et, je n'ai pas relu le topic, mais il me semble que tu étais arrivé à trouver une preuve.
Salut nightmare !
Oui oui je m'en souviens et c'est d'ailleurs la seule question que j'ai faite ici , et franchement je n'aurais
pas pu sortir la preuve tout seul :marteau:
PS. Il semblerait aussi (d'après ce que l'on m'a dit) que ces exos soient "classique" au sens où on est censé les croiser au moins une fois ... ( il me semble que quand tu avais posé l'exo la dernière fois Ben avait dit que c'était une question "classique", enfin "connue" )
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 19:13
par Nightmare » 20 Déc 2010, 19:13
Sinons :
1) C'est tellement "évident" ( une demi-ligne) que je te laisse continuer à chercher
2) Partir de
}{P(x)}=\Bigsum_{k=1}^{deg(P)} \frac{1}{x-\alpha_{k}})
(les alpha étant les racines de P)
je réfléchis au reste
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 19:17
par Nightmare » 20 Déc 2010, 19:17
Pour 5) je ne sais pas si ça se résout vraiment à un niveau "'élémentaire". On a bien une preuve via la théorème de Mason (je crois qu'on en avait déjà discuté sur le forum), le connais-tu?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 20 Déc 2010, 19:19
par Zweig » 20 Déc 2010, 19:19
Salut,
Un lemme fort utile pour le 2. :
}{P'(x)} = \sum^{\deg\,P}_{i=1} \frac{1}{x-r_i})
avec
)
les racines de

Il se trouve qu'on peut (sauf bêtise, j'ai pas de feuille sous la main..) le réutiliser au 3., b) avec
 = z^{n} - 1)
(en particularisant à z=1)
EDIT : C'est pas jusqu'à k = n-1 d'ailleurs ?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Déc 2010, 19:35
par benekire2 » 20 Déc 2010, 19:35
Nightmare > Non je ne connais pas le théorème de Mason,
Et merci pour l'indic pour le 2 ; je vais chercher , ( En fait , j'ai même trouver , une ligne .. )
Pour le 1 , je pense que le seul polynôme P possible est P(X)=X , et pour le prouver je pense qu'il va falloir étudier la composée avec les Q=X^n
PS. Zweig > si , je corrige tout de suite ;
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 20 Déc 2010, 19:37
par Le_chat » 20 Déc 2010, 19:37
Pour la 1, il y a beaucoup plus rapide (je pense qu'on y arrive avec les X^n, déjà le X^2 restreint bien les possibilités) si tu utilisais les polynômes les plus "simples" que tu connais? :lol3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 19:37
par Nightmare » 20 Déc 2010, 19:37
benekire2 a écrit:
Pour le 1 , je pense que le seul polynôme P possible est P(X)=X , et pour le prouver je pense qu'il va falloir étudier la composée avec les Q=X^n
Non il y a beaucoup beaucoup beaucoup plus simple. X est effectivement le seul polynôme solution.
Edit : Au passage, l'identité n'est pas seulement le seul polynôme possible, c'est même la seule fonction possible (preuve identique en remplaçant P par f :lol3: )
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 19:38
par Nightmare » 20 Déc 2010, 19:38
Zweig a écrit:Salut,
Un lemme fort utile pour le 2. :
}{P'(x)} = \sum^{\deg\,P}_{i=1} \frac{1}{x-r_i})
avec
)
les racines de

Attention, c'est P'/P et non P/P' :happy3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Déc 2010, 19:51
par benekire2 » 20 Déc 2010, 19:51
Pour la 1 , je prends Q les polynômes constants , PoQ=P(k) pour kR et QoP=k ainsi par différence P(k)-k=0 pour tout k dans R, ça fait bien trop de racines, P=X.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 20 Déc 2010, 19:51
par Zweig » 20 Déc 2010, 19:51
Oulà oui en effet, j'me disais bien qu'il y avait un bug pour le résultat, je toruvais 0 ...
EDIT : Sinon c'est
 = x^{n-1}-1)
à considérer.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 19:54
par Nightmare » 20 Déc 2010, 19:54
benekire2 a écrit:Pour la 1 , je prends Q les polynômes constants , PoQ=P(k) pour kR et QoP=k ainsi par différence P(k)-k=0 pour tout k dans R, ça fait bien trop de racines, P=X.
Pourquoi en viens-tu à parler des racines? Tu as montré que quel que soit x réel, P(x)=x ... Ca suffit non? Et comme je l'ai dit, ça permet de voir que le résultat n'a absolument rien à voir avec le fait que P est un polynôme.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Déc 2010, 20:03
par benekire2 » 20 Déc 2010, 20:03
Nightmare a écrit:Pourquoi en viens-tu à parler des racines? Tu as montré que quel que soit x réel, P(x)=x ... Ca suffit non? Et comme je l'ai dit, ça permet de voir que le résultat n'a absolument rien à voir avec le fait que P est un polynôme.
Oui ça suffit d'avoir montré que P(x)=x pour tout x réel, j'ai simplement dit que avec ça P(X)-X a une infinité de racine, donc est nul.
Sinon, je regarde le 3 ; et j'ai comme l'impression que le but du jeu ça va être de trouver un polynôme tel que chaque expression dans les produits soient des racines de ce polynôme et puis d'utiliser les formules de Viète.
Sinon, le 5 on le laisse de côté pour .. juste après :zen:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 20 Déc 2010, 20:06
par Zweig » 20 Déc 2010, 20:06
Pour le 3a), j'ai eu exactement la même idée dès que j'ai vu l'argument des cos² (ça m'a fait pensé à l'exercice de zeta(2) avec la somme des 1/cos²
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Déc 2010, 20:09
par benekire2 » 20 Déc 2010, 20:09
Zweig a écrit:Pour le 3a), j'ai eu exactement la même idée dès que j'ai vu l'argument des cos² (ça m'a fait pensé à l'exercice de zeta(2) avec la somme des 1/cos²
Bah je me crois avoir lu quelque part que de la méthode utilisée pour le calcul de Zeta 2 ou un truc similaire genre étude de P(X)=(X+i)^n-(X-i)^n on en déduit
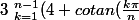))
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Déc 2010, 20:16
par benekire2 » 20 Déc 2010, 20:16
Bon j'ai la solution pour la 3b : Le produit vaut
})
Suffit alors de connaître le produit de ses sinus, que l'on connait assez bien en étudiant le polynôme Pn tel que (X-1)Pn=(X^(n+1)-1)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 20:19
par Nightmare » 20 Déc 2010, 20:19
benekire2 a écrit:Oui ça suffit d'avoir montré que P(x)=x pour tout x réel, j'ai simplement dit que avec ça P(X)-X a une infinité de racine, donc est nul.
Oui j'ai bien compris, mais à quoi cela sert-il de dire cela? Si c'est pour montrer que P(X)=X alors tu l'avais déjà fait avant d'écrire cette phrase ! Je ne comprends vraiment pas.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 20 Déc 2010, 20:33
par benekire2 » 20 Déc 2010, 20:33
Nightmare a écrit:Oui j'ai bien compris, mais à quoi cela sert-il de dire cela? Si c'est pour montrer que P(X)=X alors tu l'avais déjà fait avant d'écrire cette phrase ! Je ne comprends vraiment pas.
Oui je comprends, si P colle à Q=X sur R alors forcément P=X ; c'est que pour moi un polynôme n'accepte pas que les réels comme "entrée" puisque ça accepte beaucoup d'autres choses , après la caractérisation par l'infinité du nombre de racine m'assure que P vaut bien X.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Déc 2010, 20:42
par Nightmare » 20 Déc 2010, 20:42
"un polynôme n'accepte pas que les réels comme entrée", qu'entends-tu par là?
Ici, comme je l'ai dit le fait que P soit un polynôme on s'en fout royalement. Tu as une application P et tu as montré qu'elle envoie tout réel x sur lui même donc c'est par définition l'identité sur R point barre, pas besoin de parler de racines, d'entrée ou de je ne sais quoi. :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
