"étudier la forme" d'une fonction

[informix]

Salut à tous,
J'ai une question qui est un peu vague, je vous le dis dès maintenant :)
Je veux connaître les moyens mathématiques qui me permettent "d'étudier la forme" d'une fonction numérique réelle f: IR^n --> IR.

Pour le moment je me limite au cas où f est continue.

Aidez-moi à donner un sens plus clair à l'expression "étudier la forme" :)

Ca peut être quoi?
- convexité, concavité? ==> gradient!
- dérivabilité??
- ... ?

merci d'avance.

[busard_des_roseaux]

bjr,
le cadre de ta question est, semble-t-il , la topologie générale:
dans un espace topologique, un sous-ensemble peut être
connexe (=d'un seul morceau)
convexe (deux points quelconques peuvent être reliés par un segment de droite)
simplement connexe (=sans trou)
étoilé (il existe un point qui peut être relié à tous les autres par un segmnt de droite)
ouvert,fermé,compact,etc...

Quant à la forme, elle se définit comme ce qui est invariant par changement d'échelle , par similitude.


les principales propriétés des fonctions sont:
continuité,différentiabilité,classe ,analycité,mesurabilité...


La "forme" d'une fonction, a-priori, c'est difficile à définir. :doh:

[informix]

merci: vous avez bien situé la question dans un contexte mathématique plus rigoureux que le mien. Vous avez aussi proposé plusieurs termes intéressants.

Comme vous l'avez dit: "la forme" d'une fonction est difficile à décrire.

Si par exemple on vous donne une fonction numérique sous forme de "boite noire", a (black-box function/problem) de telle façon que vous ne pouvez calculer f(x) qu'à partir d'un ensemble discret et fini de points {x}. Comment vous pouvez avoir une idée sur la fonction f à partir des échantillons {(x,f(x)}?

[busard_des_roseaux]

re,

le problème cité a reçu plusieurs solutions dans des domaines divers des mathématiques:

On se donne n+1 points pour (1)


1) Il existe un et un seul polynôme P de degré n vérifiant
pout tout
Il s'agit du polynôme d'interpolation de Lagrange.

Malheureusement, quand on augmente le nombre de points, le procédé
ne converge pas sur les bords de l'intervalle (phénomène de Runge).

Il y a une façon optimale de choisir les (n+1) points: comme les zéros
du polynôme de Tchebycheff de degré n+1. Voilà, si l'on a le choix des
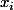et que l'on cherche une solution f, vérifiant
exactement les égalité (1).

2) si la famille sont par exemple des mesures physiques, on préfère obtenir une courbe qui passe "en moyenne" au plus près des points, qui épouse la forme du nuage de points. Il s'agit alors
d'un problème d'optimisation linéaire, appelé la "méthode des moindres carrés".
l'idée en est fort simple:

On essaye de trouver le minimum de la fonctionnelle


on peut choisir pour f des fonctions affines du type f(x)=ax+b
ou f(y)=ay+b, où l'on fait varier les coefficients a et b,
ou toute autre famille de fonctions f souhaitable adaptée au problème.

3) Une idée , que je n'ai jamais piochée, serait de passer par les différences finies.

Dans le doute, choisir la méthode (2) . Elle permet d'utiliser les statistiques
et la théorie des estimateurs.


cordialement,

[informix]

Je vous remercie bcp!
Vous avez proposé pas mal de solutions.
Je vais essayer d'étudier chacune d'elles et vous mettre au courant de ce que j'ai obtenu.