étude d'une fonction :s

par **misdirect** » 21 Sep 2009, 17:42

bonjours a tous, j'ai quelque difficulté pour la seconde partie de mon devoir qui est une étude de fonction (banal mais je galère toujours :cry: )

Soit f la fonction définie sur l'intervalle ] 0 ; +l'infini [ par f(x) = x² (1-lnx) si x >0 et f (0) = 0

On admettra que f est dérivable en 0 <( pas compri ça) et que f'(0)=0 on note C la courbe représentative de f dans un repère orthnormal (o i j)

* montrer que pour tout x de ] 0 ; + l'infini [, f'(x)= x(1-2lnx)
* étudier le signe de 1 - 2 lnx <<< pour sa je dérive ? et je rentre la fonction dans "graph" de ma casio pour voir si la courbe monte ou descend soit je pourrai dire + ou - ? ou ce n'est pas la bonne méthode?>>>
*En déduire le sens de variation <<< sa quand j'aurai trouver le signe je sais faire>>>

*calculer la limite de f(x) lorsqu'il tend vers + l'infini on admet que
lim f(x) = 0
x->0

la dernière je ne me souviens plus de la méthode...

voila si quelqu'un pouvais m'éclaircir les idées sa m'avancerai,
mon niveau en math étant médiocre je sens que le bts vas me passer sous le nez :( en espérant remonter les notes ailleurs...a

par **melreg** » 21 Sep 2009, 17:57

misdirect a écrit:On admettra que f est dérivable en 0 >>

Pas besoin. Tu dois juste voir quand est-ce que

s'annule, quand est-ce qu'il est positif et quand est-ce qu'il est négatif. Pour cela, il faut connaître la fonction

.

misdirect a écrit:*En déduire le sens de variation >>

Tu peux dériver, ou simplement regarder si la fonction croît, ou décroît.

misdirect a écrit:*calculer la limite de f(x) lorsqu'il tend vers + l'infini on admet que
lim f(x) = 0
x->0

la dernière je ne me souviens plus de la méthode...

A nouveau, il faut savoir comment se comporte

(notamment). Une limite sert à savoir comment se comporte une fonction, généralement au bord du domaine (comme ici 0 ou

).

Bon courage...

par **misdirect** » 21 Sep 2009, 18:06

okey je vois plus ou moins...

pour savoir comment la fonction s'annule je dois faire "ma fonction = 0" ?
avec la calculette il y a posibilité avec la fonction "tabl" ? j'ai beaucoup de mal désolé si mes questions son bètes...

après réflexion je trouve sa pour les 2 premier astérix

x | 0 ? +'linfini
______________________________________
f(x) | + | -
_________________________________________
f'(x) | fleche vers le o ? fleche vers le bas

par contre d'après l'énnoncé dois je trouver les deux valeurs qu'il doit y avoir
aux endroit ou j'ai mis les "?"

sinon ma reflexion est juste ?
merci

par **melreg** » 21 Sep 2009, 18:26

Ta réflexion est juste. Les points d'interrogations correspondent au second point où ta fonction s'annule.

Par contre, prends l'habitude de ne pas utiliser la calculatrice... cet exercice est faisable sans elle...

par **misdirect** » 21 Sep 2009, 18:35

daccord merci

comment je peut faire sans calculatrice?

pour trouver mes deux points d'intérogation comment je fais?

par **melreg** » 21 Sep 2009, 18:41

Sans calculatrice, il faut connaître quelques propriétés de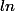

.

Pour les points d'interrogation, ça peut être soit la valeur de

pour que ta fonction s'annule. Ou alors pour que la dérivée de ta fonction s'annule, ... . Je ne sais pas, mais c'est généralement des questions "intéressantes" qu'on peut se poser...

par **misdirect** » 21 Sep 2009, 18:46

okey oui je regarderai donc les propriétés de ln,
pour connaitre la limite de x qui tend vers 0 la j'ai vraiment aucune idée :s

par **melreg** » 21 Sep 2009, 18:56

Par tâtonnements, on peut se dire que comme la fonction est dérivable (à droite en 0 notamment), elle est continue en 0. D'où la valeur de la limite.
Une autre façon de faire est de savoir que

(il y a une proposition qui dit ça).
Encore une autre façon est de procéder est d'utiliser la règle de L'Hospital.

Mais ça demande certaines connaissances. Peut-être que tu les verras bientôt?!

étude d'une fonction :s

étude d'une fonction :s

Qui est en ligne