Etude de graphe

par **biba06** » 16 Sep 2010, 15:33

Bonjour à tous,

J'ai un petit problème à résoudre niveau IUT et je bute dessus.

Soit C0 l'ensemble des sommets de niveau 0, donc sans prédécesseur. On supprime dans le graphe tous les sommets de C0 ainsi que les arcs qui s'appuient sur ces sommets. On obtient un sous-graphe G1.
Soit C1 l'ensemble des sommets de G1 sans prédécesseur. Ce sont les sommets de niveau 1 de G. On supprime dans le graphe G1 tous les sommets de C1 ainsi que les arcs qui s'appuient sur ces sommets. On obtient un sous-graphe G2.
On réitère ce procédé tant qu'il reste des sommets.
Ce procédé permet de déterminer les niveaux des sommets d'un graphe sans circuit.

Question 16 : Décrire un procédé qui permet de caluler, pour chaque sommet de numéro s, le nombre de prédécesseurs. Le graphe est donné par sa matrice d'ajacence M[i,j]. De manière analogue, donner le procédé qui permet de calculer le nombre de successeurs de s.

J'ai essayé d'y réfléchir. Je pars de la matrice d'adjacence qui me donne les successeurs d'un graphe quelconque. Je prend un sommet et détermine son niveau (nombre de chemin le plus long pour arriver au sommet en question). Et je soustrais le niveau au nombre de successeurs. Mais cette idée n'est pas très logique néanmoins et ne marche pas tout le temps.

Est ce que quelqu'un peut m'aider ?

par **biba06** » 16 Sep 2010, 20:06

Personne n'a une petite idée ? TT_TT :cry:

par **busard_des_roseaux** » 17 Sep 2010, 07:48

Bonjour,

je sais pas trop. L'idée à priori, c'est que si le graphe est représenté par une matrice A, avec

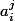= nombre d'arêtes du sommet i vers j

peut être les puissances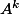

de cette matrice A donneront un nombre de chemins

essaye aussi de transporter, de traduire les propriétés d'algèbre linéaire (sous matrice de A de rang r, trace,sous espace propres, etc..) en propriétés topologiques du graphe.

par **fatal_error** » 17 Sep 2010, 08:04

salut,

qu'entend-t-on par prédecesseur/successeur d'un sommet?

par **biba06** » 17 Sep 2010, 17:14

je vérifie votre idée busard des roseaux. Un prédécesseur est le sommet qui précède un sommet s et son successeur celui qui suit ce sommet s. :) merci je vais voir tout et vous tiens au courant.

par **fatal_error** » 17 Sep 2010, 19:25

La question que je sous entendais est par exemple si on a
1->2->3, est-ce que 3 est un successeur de 1, ou pas.

parce que si on prend (dans le vrai terme) les successeurs de 1, il n'y a que 2.
Et si c'est bien ces notions genre "le plus proche" suivant/précédent, alors c'est directement donné par la matrice d'adjacence, et la notion de niveaux, on s'en tamponne!

par **biba06** » 17 Sep 2010, 21:34

Je suis d'accord avec, effectivement la matrice d'adjacence donne à la fois les successeurs et prédécesseurs (directs) mais c'est le mot calculer qui me gêne dans la question... :s

Autre question j'ai un graphe G3 non connexe à 10 sommets.
On me demande de donner les 4 composantes connexes du graphe.
Je voulais savoir ce que vous pensez de mes réponses. =)

http://img137.imageshack.us/img137/4273/graphenonconnexea10somm.jpg
http://img707.imageshack.us/img707/7056/quatrecomposantesconnex.jpg

par **fatal_error** » 18 Sep 2010, 00:45

salut,

nan, il sagit des groupes "isolés", du genre
{x0,x1,x2,x4};{x8}...etc

la composante c'est genre le sous graphe en fait, un peu comme un selectionner/couper

par **biba06** » 18 Sep 2010, 11:37

Dans mon graphe G3 ils sont donnés donc les composantes connexes, il s'agit de:
(x0,x1,x2,x3,x4) (x8) (x9,x10) (x5,x6,x7)

Pensez vous que dans l'énoncé: "Décrire un procédé qui permet de calculer..." faut il effectuer un calcul car si l'on s'appuie que sur la matrice d'adjacence, on remarque qu'il n'y a pas besoin de calculer justement.

par **fatal_error** » 18 Sep 2010, 12:17

vu que tu es a la question 16, pe que les histoires de niveaux concernent d'autres questions.

Etant assez basique, moi jferais la somme des 1 présent dans une ligne de la matrice d'adjacence (resp colonne). Quit à cque ca soit "trop simple".

par **biba06** » 18 Sep 2010, 12:50

C'est bien ce que je pensais ça a l'air trop simple mais c'est surement ça puisque ça marche. :) et dans mon graphe G3 pensez vous que pour les composantes connexes, il s'agit de:
(x0,x1,x2,x3,x4) (x8) (x9,x10) (x5,x6,x7).

Merci beaucoup pour votre aide :)

par **fatal_error** » 18 Sep 2010, 13:14

re,

ui pour moi.

par **biba06** » 19 Sep 2010, 21:36

OK merci beaucoup je crois que c'est tout pour les graphes ;)

Etude de graphe

Etude de graphe

Qui est en ligne