Etude de fonctions

[pikaaa]

Bonjour,

J'ai un devoir préparé sur les études de fonctions.

maths.PNG (11.32 Kio) Vu 246 fois

Je dois:
a) trouver le domaine de définition
b) montrer que f est continue en 0
c) justifier la dérivabilité de f pour x différent de 0

Cependant je bloque sur la question b. J'ai tenté de trouver la limite de f en 0 avec toutes sortes de techniques (théorème de l'Hôpital, quantité conjuguée, factorisation), rien à faire je ne sais pas tellement d'où partir.
Auriez-vous une idée ?

Merci de vos futures réponses !

[infernaleur]

Salut, pourtant multiplier par la quantité conjuguée ça marche plutôt bien (si on multiplie par le bon truc ^^) :



[on remarque bien sur immédiatement que au numérateur on peut utiliser la fameuse formule (a-b)(a+b)=a²-b² donc pas la peine de tout développer]

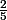
Et quand tu simplifies tout ça tu obtiens à la fin sauf erreur : qui tend bien vers quand x tend vers 0.

[LB2]

Bonsoir,

si tu connais les développements limités, on peut aussi directement calculer un DL à l'ordre 2 en 0 du numérateur (6/5 x^2 + o(x^2)) qui permet de conclure à l'existence et à la valeur de la limite de f en 0.

et cela te donnerait même la dérivabilité de f en 0 (en remarquant qu'en fait on n'a pas seulement f(x)=2/5+o(1), mais même f(x)=2/5+O(x^2) au voisinage de 0, ce qui permet de conclure en formant le taux de variation en 0).

[pikaaa]

Merci beaucoup pour vos réponses ! J'ai compris