étude d'arcsin

[sociaux]

bonjour, j'étudie la fonction f(x) = arcsin x
1° J'ai montré que sa dérivée n-ième valait Pn(x) / (1-x²)^(n-1/2) avec Pn polynome. j'ai aussi (1-x²) f"(x) = x f'(x) mais je bloque pour déduire une relation entre Pn, Pn+1 et Pn+2 d'après formule de Leibniz.
2) Soit bn = dérivée n-ième de f en 0. Il faut montrer b2n = 0 et b2n+1 = [(2n)!/ (2^n n!)]² et là non plus je sais pas comment faire. merci par avance

[Pythales]

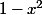
Si tu appliques la formule de Leibniz à l'ordre , le terme en disparait après 2 dérivations, et le terme en au bout d'une dérivation, ce qui donne bien une récurrence sur 3 termes

[sociaux]

oui en effet, je suis un peu idiot sur ce coup là.. pour la 2, la relation de récurrence est-elle à utiliser ?

[sociaux]

pour info j'ai (n²-n+1)Pn/(1-x²)^(n-1/2) - 2xnPn+1/(1-x²)^(n+1/2)-Pn+2/(1-x²)^(n+1/2). Est-ce cela ?

[sociaux]

je vois toujours pas pour la2)..

[sociaux]

Pour bn ,pas de lien avec la récurrence? Merci

[sociaux]

merci de l'aide par avance!