Qu'est ce que des boréliens?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par absolut-diabolik » 26 Déc 2011, 08:54
par absolut-diabolik » 26 Déc 2011, 08:54
Rassurez vous j'ai lu la définition : éléments de la tribu borélienne qui est la tribu engendrée par les ouvert de R mais concrètement j'arrive pas à voir ce que c'est.
Je sais que les pavés ouverts, les pavés fermés sont des boréliens. souvent en exercice pour montrerqu'un ensemble est un borélien on utilise une fonction réciproque, tout ça j'ai "compris".
Mais là je séche complétement sur un exercice, je ne sais pas par où commencer et la définition ne m'inspire pas du tout!

K l'ensemble triadique de Cantor
http://fr.wikipedia.org/wiki/Ensemble_de_Cantor1. Montrer que


sont des boréliens...
Pour

, j'ai écrit

où P est réunion dénombrable de pavés ouverts. ainsi

est réunion dénombrables de boréliens => borélien!
2. Pour tout

calculer


est (bien sûr) la mesure de Lebesque
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2011, 11:22
par girdav » 26 Déc 2011, 11:22
Bonjour,
c'est quoi

?

privé de

?
Pour
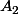
et
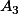
on se sert du fait que

est dénombrable et que les singletons sont des boréliens.
 par absolut-diabolik » 26 Déc 2011, 14:58
par absolut-diabolik » 26 Déc 2011, 14:58
Oui R privé de K.
Je sais que Q est borélien mais R privé de Q reste quand même une réunion de singletons n'est ce pas?
Et que penser que K+ Q est ce que K est un borélien (peut être que oui parcve que c'est une réunion de pavés fermés)
girdav a écrit:Bonjour,
c'est quoi

?

privé de

?
Pour
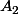
et
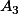
on se sert du fait que

est dénombrable et que les singletons sont des boréliens.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2011, 15:17
par girdav » 26 Déc 2011, 15:17
absolut-diabolik a écrit:Je sais que Q est borélien mais R privé de Q reste quand même une réunion de singletons n'est ce pas?
Oui, mais une union non dénombrable, donc on n'est pas sûr. Par contre, le complémentaire d'un borélien est encore un borélien.
Et que penser que K+ Q est ce que K est un borélien (peut être que oui parcve que c'est une réunion de pavés fermés)
On peut écrire que

puis montrer que

est un borélien, ce qui n'est pas difficile une fois que l'on a vu que

en est un.
 par absolut-diabolik » 26 Déc 2011, 18:52
par absolut-diabolik » 26 Déc 2011, 18:52
Merci je viens de comprendre ! Mais juste une petite précision k est un borélien pour la raison que j'ai donné c'est bon ? (ensemble de pavés ouverts?).
Merci de ton aide
girdav a écrit:Oui, mais une union non dénombrable, donc on n'est pas sûr. Par contre, le complémentaire d'un borélien est encore un borélien.
On peut écrire que

puis montrer que

est un borélien, ce qui n'est pas difficile une fois que l'on a vu que

en est un.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2011, 19:24
par girdav » 26 Déc 2011, 19:24
Qu'est-ce qu'un "pavé" de

? Intervalle ? Dans ce cas, c'est plus ou moins ça puisque l'on peut écrire

comme une intersection dénombrable d'union d'intervalles fermés.
 par absolut-diabolik » 26 Déc 2011, 19:46
par absolut-diabolik » 26 Déc 2011, 19:46
Oui oui je parlais bien d'intervalles! Je pense avoir compris.
en ce qui concerne les intégrales.
J'ai réussi à faire la 2ème (la plus facile

)
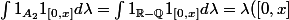-\lambda (\mathbb{Q}\cap[0,x])=x)
car Q est de mesure de Lebesgue nulle.
Les deux autres j'ai du malo déjà parce que de mon avis K est inclus dans Q. donc je n'arrive pas à identifier l'ensemble K+Q. Et de même avec A1, l'intersection avec [0,x] n'est pas évidente.
girdav a écrit:Qu'est-ce qu'un "pavé" de

? Intervalle ? Dans ce cas, c'est plus ou moins ça puisque l'on peut écrire

comme une intersection dénombrable d'union d'intervalles fermés.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2011, 20:06
par girdav » 26 Déc 2011, 20:06

ne peut être inclus dans

puisqu'il n'est pas dénombrable, mais par contre il est de mesure nulle, et c'est ça qu'il faudra exploiter.
 par absolut-diabolik » 26 Déc 2011, 20:17
par absolut-diabolik » 26 Déc 2011, 20:17
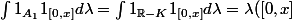-\lambda (K\cap[0,x])=x)
car K est de mesure de Lebesgue nulle.
C'est exactement la même chose que la 2ème alors ?
girdav a écrit:
ne peut être inclus dans

puisqu'il n'est pas dénombrable, mais par contre il est de mesure nulle, et c'est ça qu'il faudra exploiter.
 par absolut-diabolik » 26 Déc 2011, 20:19
par absolut-diabolik » 26 Déc 2011, 20:19
Mais je buggue totalement pour la 3ème.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2011, 20:31
par girdav » 26 Déc 2011, 20:31
Donne-toi

une énumération des rationnels.

, et chacun de ces ensembles est de mesure nulle.
 par absolut-diabolik » 26 Déc 2011, 20:39
par absolut-diabolik » 26 Déc 2011, 20:39
Mais c'est l'intersection avec [0,x] qui me pose problème. Comment identifier les élements de cet intervalle qui est dans K+Q?
girdav a écrit:Donne-toi

une énumération des rationnels.

, et chacun de ces ensembles est de mesure nulle.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2011, 20:41
par girdav » 26 Déc 2011, 20:41
Si on montre que

est de mesure nulle, cet ensemble intersecté avec
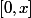
le sera à plus forte raison.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
