Est - il facile de résoudre cette équation ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Fév 2015, 21:32
par barbu23 » 12 Fév 2015, 21:32
Bonjour à tous,
D'après un petit calcul simple, on arrive aux formules suivantes :
!} \Big) + \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_0 (x) + A_1 (x) + A_2 (x) \\ e^{jx} = \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n}}{(3n)!} \Big) + j \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + j^2 \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_{0} (x) + j A_{1} (x) + j^2 A_2 (x) \\ e^{j^{2} x} = \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n}}{(3n)!} \Big) + j^2 \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + j \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_{0} (x) + j^2 A_{1} (x) + j A_2 (x) \end{cases})
avec :

.
Cela implique que :
 = \displaystyle \sum_{n \geq 0} \frac{x^{3n}}{(3n)!} = \frac{1}{3} ( e^{x} + e^{jx} + e^{j^{2} x } ) \\ A_1 (x) = \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} = \frac{1}{3} ( e^{x} + j^2 e^{jx} + j e^{j^{2} x } ) \\ A_2 (x) = \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} = \frac{1}{3} ( e^{x} + j e^{jx} + j^2 e^{j^{2} x } ) \end{cases})
Ma question est la suivante :
Pourriez vous m'indiquer une méthode qui permet de trouver :

et

dans

en fonction de

tels que :
 + jA_1 (a) ) ( A_0 (b) + j^2 A_1 (b) ))
Merci infiniment pour votre aide.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 13 Fév 2015, 10:06
par jlb » 13 Fév 2015, 10:06
Salut, ta première égalité, cela donne quoi pour x=0?
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 13 Fév 2015, 12:35
par paquito » 13 Fév 2015, 12:35
barbu23 a écrit:Bonjour à tous,
D'après un petit calcul simple, on arrive aux formules suivantes :
!} \Big) + \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_0 (x) + A_1 (x) + A_2 (x) \\ e^{jx} = \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n}}{(3n)!} \Big) + j \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + j^2 \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_{0} (x) + j A_{1} (x) + j^2 A_2 (x) \\ e^{j^{2} x} = \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n}}{(3n)!} \Big) + j^2 \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + j \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_{0} (x) + j^2 A_{1} (x) + j A_2 (x) \end{cases})
avec :

.
Cela implique que :
 = \displaystyle \sum_{n \geq 0} \frac{x^{3n}}{(3n)!} = \frac{1}{3} ( e^{x} + e^{jx} + e^{j^{2} x } ) \\ A_1 (x) = \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} = \frac{1}{3} ( e^{x} + j^2 e^{jx} + j e^{j^{2} x } ) \\ A_2 (x) = \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} = \frac{1}{3} ( e^{x} + j e^{jx} + j^2 e^{j^{2} x } ) \end{cases})
Ma question est la suivante :
Pourriez vous m'indiquer une méthode qui permet de trouver :

et

dans

en fonction de

tels que :
 + jA_1 (a) ) ( A_0 (b) + jA_1 (b) ))
Merci infiniment pour votre aide.
quel est le but du jeu?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Fév 2015, 16:22
par barbu23 » 13 Fév 2015, 16:22
paquito a écrit:quel est le but du jeu?
Je m'excuse, je modifie un petit peu l'énoncé pour mon besoin :
Le but du jeu est de trouver précisément deux fonctions :
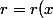)
et
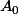
telle que :
 ( A_0 (y) + A_0 ' ( y ) ) ( A_0 ( z ) + A_0 '' ( z ) ) = e^{x+y+z} \\ r (x) ( A_0 (y) + j A_0 ' ( y ) ) ( A_0 ( z ) + j A_0 '' ( z ) ) = e^{x+jy+j^{2} z} \\ r (x) ( A_0 (y) + j^2 A_0 ' ( y ) ) ( A_0 ( z ) + j^2 A_0 '' ( z ) ) = e^{x+ j^{2} y + j z} \end{cases})
C'est donc un système d'EDO à variables séparables il me semble.
Est ce possible de le faire ?
Merci d'avance. :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
!} \Big) + \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_0 (x) + A_1 (x) + A_2 (x) \\ e^{jx} = \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n}}{(3n)!} \Big) + j \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + j^2 \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_{0} (x) + j A_{1} (x) + j^2 A_2 (x) \\ e^{j^{2} x} = \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n}}{(3n)!} \Big) + j^2 \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+1}}{(3n+1)!} \Big) + j \Big( \displaystyle \sum_{n \geq 0} \frac{x^{3n+2}}{(3n+2)!} \Big) = A_{0} (x) + j^2 A_{1} (x) + j A_2 (x) \end{cases})
.
et
dans
en fonction de
tels que :
 + jA_1 (a) ) ( A_0 (b) + jA_1 (b) ))