Besoin d'aide pour un exercice censé être facile ! (c'est im

[Florix]

Bonjour,

Voilà, il faudrait dans l'idéal que je puisse comprendre les raisonnements à appliquer dans cet exo pour demain, ceci dit je n'arrive pas les questions

2 /

3 /

4 /

Voici l'énoncé : CLIQUEZ ICI ou copier directement le lien dans la barre d'adresse
http://hebergerimage.free.fr/show.php/43367/scan0002.jpg

Dans la correction de la question 2 / il est écrit Un = n + 1 mais cette somme ne converge pas vers 0 je ne comprends pas !

Merci d'avance pour vos réponses

[abcd22]

Pour le 2/, si on prend x_n = n + 1 il y a des simplifications dans le produit et on trouve .
3/ Pour faire le 1/ tu as certainement utilisé le logarithme pour avoir des séries.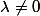 équivaut à converge. Et comme et que ces suites sont positives on a l'équivalence du 3.
4/ On peut minorer x_n par la suite géométrique (récurrence), ce qui permet de montrer que converge (puisque x_0 > 1).

[Florix]

Merci je vais potasser ça !

Unique problème : j'ai pas utilisé le log dans la question 1, j'ai montré que 0 < Un < 1 puis on passe à la limite !

Je veux bien ta solution avec les log !

Merci abcd22 pour tous tes messages d'aide

PS : j'apprends tjs doucement mais surement le chinois avec le Belassen sur tes bons conseils

[abcd22]

Oui ça marche aussi en disant que c'est décroissant minoré en fait.
Sinon on écrit que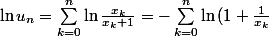 , la suite ln(u_n) est décroissante et strictement négative donc tend vers une limite finie <0 ou vers , et en repassant à l'exponentielle on a le résultat sur u_n.

Moi je fais une petite pause dans le chinois pour cause d'écrits d'agrég très très bientôt là...(mercredi et jeudi) D'ailleurs je vais peut-être aller dormir.

[Florix]

Ah bah bon courage encore pour les écrits et bonne nuit !

Moi je vais aller suivre tes bons conseils pour mon exo ! Encore un grand merci !

A bientot sur maths-forum !

[Florix]

ps : sans etre indiscret c'est quoi tes ecrits d'agreg ?

bonne nuit !