A est dense dans U

[Lostounet]

Bonjour,

Je souhaite montrer que l'ensemble
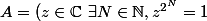est dense dans U (ensemble des z de module 1)
Je souhaite aussi savoir si cela me permet de dire en toute confiance qu'il existe des points de U en lesquels je ne peux pas centrer une boule ouverte (qui n'intersecte pas A)

Voici des pistes:

1. Prendre un élément u quelconque dans U et montrer qu'il existe un élément de A aussi proche de u que voulu

2. Utiliser la définition topologique de la densité: tout point de U est-il limite d'une suite de points de A?

3. (plus philosophique) Est-il possible de "transporter" la densité de R dans C par une application? Dans mon cours, l'exponentielle complexe a "renvoyé" les droites verticales sur des cercles.
Puis-je transporter l'éventuelle densité sur un axe vertical (d'un ensemble A' qui serait en quelque sorte l'antécédent de mon A) par une application comme exp?

Merci

[Ben314]

Autre piste :
0) Résoudre dans C l'équation et (quasi directement) conclure.

Quand à ton 3) parlant de "la densité de R dans C", j'ai un peu des doutes...

[zygomatique]

salut

soit z un élément de U et a un argument de z ... donc les arguments de z sont les avec

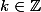
soit h > 0

on cherche donc à résoudre l'inéquation d'inconnues n, p et k ::

....

[Lostounet]

Bonjour,
Merci de vos réponses.

Avant de rentrer dans le vif du sujet, je voudrais juste éclairer le 3).
Cela n'a peut-être rien à voir mais ça m'intéresse
On sait que Q est dense dans R.
Donc iQ est dense dans iR (sur l'axe des ordonnées)

Est-ce que exp<iQ> est dense dans exp<iR>?

Tout d'abord dans mon intuition, si l'exp va enrouler tout l'axe sur le cercle unitaire, il y a deux cas de figure:
* soit on prend un ensemble de la forme k*pi/3 et son exponentielle va donner des points bien localisés sur le cercle
* soit on accumule anarchiquement des points qui seront denses dans ce cercle

Est-ce que par exemple l'ensemble des puissances de 2 est dense dans R? Non...
Et pourtant il peut bien devenir dense dans le cercle unité si je lui applique exp
...

Est-ce que mon idée passe? Ou c'est du non sens

[Doraki]

Est-ce que tu pourrais démontrer que si f est une fonction continue de B dans C, et A est dense dans B alors f(A) est dense dans f(B) ?

[Lostounet]

Oui, soit b quelconque dans B
Il existe (an) qui converge vers b
Donc par continuité de f sur B f(an) en l'infini c'est f(b)

Mais là c'est pas exactement cela que je veux: je veux prendre l'image d'un truc V a priori non dense dans B
Et que f(V) soit dense dans f(B) malgré tout sous des hypothèses supplémentaires sur f (l'exponentielle).

Les puissances de 2 sont "de plus en plus espacés" sur R, alors que exp(i*2^N) me semblent denses sur le cercle

[zygomatique]

N n'est pas dense dans R et pourtant cos (N) est dense dans cos (R) ....

[Ben314]

... que exp(i*2^N) me semblent denses sur le cercle

Perso, je ne vois pas le moindre rapport entre les exp(i*2^N) et le problème initial...

0) Résoudre sans se gourer dans C l'équation et (quasi directement) conclure.