bonjour,
je fais un mémoire sur l'espace des fonctions à support compact dense dans l'espace Lp. J'ai déjà effectué la démonstration mais je n'ai aucune idée d'extension et d'applications possibles...si vous aviez une piste à me donner...
merci!
Mémoire sur "Cc(Rn) dense dans Lp"
3 messages
- Page 1 sur 1
Bonsoir,
la densité de dans
dans 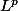 peut être utilisée pour démontrer que pour toute fonction
peut être utilisée pour démontrer que pour toute fonction  de
de ) , l'application de
, l'application de 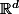 dans
dans ) qui à
qui à  associe l'application
associe l'application ) est unifromément continue. Ce résultat permet de montrer que si
est unifromément continue. Ce résultat permet de montrer que si 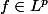 et
et 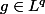 , avec
, avec 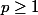 et
et  , le produit de convolution
, le produit de convolution  (où
(où  = \int_{\mathbb{R}^d} f(x-y)g(y)dy) ) est défini sur
) est défini sur 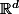 , uniformément continu et borné (on n'utilise la densité que pour l'uniforme continuité en fait, le reste vient de l'inégalité de Hölder).
, uniformément continu et borné (on n'utilise la densité que pour l'uniforme continuité en fait, le reste vient de l'inégalité de Hölder).
En utilisant la densité de , on peut aussi montrer que si
, on peut aussi montrer que si ) est une approximation de
est une approximation de 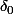 (c'est-à-dire que les fonctions
(c'est-à-dire que les fonctions 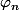 sont continues à support compact sur
sont continues à support compact sur 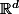 , les supports des
, les supports des 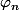 sont tous inclus dans un même compact, pout tout n,
sont tous inclus dans un même compact, pout tout n,  et
et  , et pour tout
, et pour tout 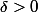 ,
,  dx =0) ), et si
), et si 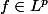 ,
, 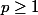 , alors
, alors  dans
dans 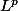 .
.
Avec le premier résultat que j'ai donné, on peut montrer que si) , alors
, alors  et
et  , où
, où 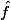 est la transformée de Fourier de
est la transformée de Fourier de  (
( = \int_{-\infty}^{+\infty} f(x) e^{-ixt} dx) ) et
) et 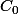 est l'ensemble des fonctions continues sur
est l'ensemble des fonctions continues sur  et tendant vers 0 à l'infini.
et tendant vers 0 à l'infini.
la densité de
En utilisant la densité de
Avec le premier résultat que j'ai donné, on peut montrer que si
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
