Espace borelien
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
guadoc
- Messages: 6
- Enregistré le: 16 Nov 2008, 15:44
-
 par guadoc » 16 Nov 2008, 15:47
par guadoc » 16 Nov 2008, 15:47
Bonjour à tous.
J'aimerais savoir quelle est la différence entre l'espace borélien ( sur R) et P(R) qui sont les parties de R.
Merci d'avance pour vos contributions.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 16 Nov 2008, 16:27
par ThSQ » 16 Nov 2008, 16:27
Il y a une énorme différence : |B|=|R| < P(R) même si c'est pas si évident de montrer un sous-ensemble non borélien.
-
mathelot
 par mathelot » 16 Nov 2008, 16:54
par mathelot » 16 Nov 2008, 16:54
ThSQ a écrit:Il y a une énorme différence : |B|=|R| < P(R) même si c'est pas si évident de montrer un sous-ensemble non borélien.
euh, je crois l'ensemble composé d'un élément de chaque classe
du quotient
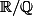
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 16 Nov 2008, 17:13
par ThSQ » 16 Nov 2008, 17:13
mathelot a écrit:euh, je crois l'ensemble composé d'un élément de chaque classe
du quotient
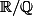
Oui oui je sais bien, c'est le contrex de Vitali, qui n'est pas mesurable, j'appelle pas ça un truc
évident (en plus du fait que ça nécessite l'Axiome du Choix)
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 16 Nov 2008, 17:34
par Antho07 » 16 Nov 2008, 17:34
J'ai entendu dire qu'il y avait un moyen de construire un ensemble non borélien de R en considérant R comme un Q-espace vectoriel et en prenant une intersection avec un hyperplan.
Quelqu'un peut-il m'éclairer sur ce sujet?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
