Equation trigonométrique et récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MrBrightside
- Membre Naturel
- Messages: 52
- Enregistré le: 05 Sep 2012, 18:12
-
 par MrBrightside » 09 Sep 2012, 15:08
par MrBrightside » 09 Sep 2012, 15:08
Salut Luc, merci de venir de nouveau à mon secours!
Donc si je comprends bien ce que tu me dis, il faut faire ce qui suit:
J'ai donc
 \geq \bigsum_{k=0}^{n} \frac{x^k}{k!})
On a donc au rang p+1,
 \geq \bigsum_{k=0}^{p+1} \frac{x^{p+1}}{k!})
Or si on divise de part et d'autre par
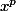
, on obtient:
}{x^p} \geq \bigsum_{k=0}^{p+1} \frac{x^{p+1}}{x^p*k(p+1)!})
Et donc par simplification on a:
}{x^p} \geq \bigsum_{k=0}^{p+1} \frac{x}{(p+1)!})
Or
!} = + \infty)
, on en déduit donc par comparaison que
}{e^x} = + \infty)
C'est juste?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Sep 2012, 15:14
par Kikoo <3 Bieber » 09 Sep 2012, 15:14
Re,
J'ai aucune piste mais je peux te dire là où ton raisonnement bloque :
Tes sommes sont indicées par la variable muette k, et non p.
La manière dont tu divise des deux côtés par
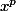
est fausse, car les
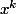
varient quand k va de 0 à p+1, tandis que p est fixe.
-
MrBrightside
- Membre Naturel
- Messages: 52
- Enregistré le: 05 Sep 2012, 18:12
-
 par MrBrightside » 09 Sep 2012, 15:25
par MrBrightside » 09 Sep 2012, 15:25
Exact, j'ai fait un peu n'importe quoi... :hum:
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 16:29
par Luc » 09 Sep 2012, 16:29
Tu as la bonne idée mais il ne faut pas s'embrouiller avec les indices ^^.
MrBrightside a écrit:Salut Luc, merci de venir de nouveau à mon secours!
Donc si je comprends bien ce que tu me dis, il faut faire ce qui suit:
J'ai donc
 \geq \bigsum_{k=0}^{n} \frac{x^k}{k!})
On a donc au rang p+1,
 \geq \bigsum_{k=0}^{p+1} \frac{x^{p+1}}{k!})
Non on a
 \geq \bigsum_{k=0}^{p+1} \frac{x^{k}}{k!})
ce qui est très différent.
MrBrightside a écrit:Or si on divise de part et d'autre par
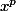
, on obtient:
}{x^p} \geq ...)
Pareil, on a plutôt
}{x^p} \geq \bigsum_{k=0}^{p+1} \frac{x^{k}}{x^p*k!})
.
A partir de la lidée est de ne garder que le terme intéressant en k=p+1 qui donne de l'information en l'infini. Le reste est positif donc tu le minores par 0.
MrBrightside a écrit:Et donc par simplification on a:
}{x^p} \geq ...)
Pareil, c'est plutôt
}{x^p} \geq \bigsum_{k=0}^{p+1} \frac{x^{k-p}}{k!})
MrBrightside a écrit:Or
!} = + \infty)
, on en déduit donc par comparaison que
}{x^p} = + \infty)
C'est juste?
Ça c'est juste. Miraculeux comme les erreurs de calcul successives s'annulent, non? ^^
-
MrBrightside
- Membre Naturel
- Messages: 52
- Enregistré le: 05 Sep 2012, 18:12
-
 par MrBrightside » 09 Sep 2012, 16:34
par MrBrightside » 09 Sep 2012, 16:34
Le reste est positif donc tu le minores par 0.
Je ne parviens pas à comprendre cette partie de ton explication. Qu'est ce que ça signifie exactement?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 16:38
par Luc » 09 Sep 2012, 16:38
MrBrightside a écrit:Je ne parviens pas à comprendre cette partie de ton explication. Qu'est ce que ça signifie exactement?
Minorer un nombre réel

c'est trouver un autre nombre réel

tel que

. Minorer un nombre réel par 0 c'est juste dire que ce nombre est positif.
Les techniques de minoration et de majoration sont essentielles pour établir des inégalités.
"Le reste" désigne les autres termes de la somme.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Sep 2012, 16:40
par Kikoo <3 Bieber » 09 Sep 2012, 16:40
MrBrightside a écrit:Je ne parviens pas à comprendre cette partie de ton explication. Qu'est ce que ça signifie exactement?
Je suis pas sûr, c'est ce qu'on appelle minoration grossière n'est-ce pas Luc ?
Pour le reste, c'est intéressant. Je prends note car j'aurais pas su cheminer ainsi

-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 16:49
par Luc » 09 Sep 2012, 16:49
[quote="Kikoo 1[/TEX], mais elle est assez bonne si

-
MrBrightside
- Membre Naturel
- Messages: 52
- Enregistré le: 05 Sep 2012, 18:12
-
 par MrBrightside » 09 Sep 2012, 16:53
par MrBrightside » 09 Sep 2012, 16:53
J'ai du mal à comprendre quoi faire exactement.
J'ai donc à la base, comme montré dans la question 1:
 \geq \bigsum_{k=0}^{p+1} \frac{x^k}{k!})
Ensuite, si je comprends bien ce que tu me dis, par minoration par 0, ça me fait
 \geq \frac{x^k}{k!})
C'est comme ça qu'il faut faire?
Ensuite je divise de part et d'autre par
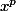
, je calcule la limite et c'est bon?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 16:57
par Luc » 09 Sep 2012, 16:57
MrBrightside a écrit:J'ai du mal à comprendre quoi faire exactement.
J'ai donc à la base, comme montré dans la question 1:
 \geq \bigsum_{k=0}^{p+1} \frac{x^k}{k!})
Oui.
MrBrightside a écrit:Ensuite, si je comprends bien ce que tu me dis, par minoration par 0
Quel réel minores-tu par 0?
MrBrightside a écrit:ça me fait
 \geq \frac{x^k}{k!})
C'est quoi k?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Sep 2012, 17:01
par barbu23 » 09 Sep 2012, 17:01
Bonjour, :happy3:
Voici la méthode générale, qui permet de résoudre ton premier exercice :
Résoudre :
 + b \sin ( x ) = c $)
En effet :
 + b \sin (x) = \sqrt{a^{2}+b^{2}} \Big( \frac{a}{\sqrt{a^{2}+b^{2}}} \cos ( x) + \frac{b}{\sqrt{a^{2}+b^{2}}} \sin (x) \Big) $)
Remarquons que :

et

Donc, il existe,

, tel que :
 $)
et
 $)
Par conséquent :
 + b \sin (x) = \sqrt{a^{2}+b^{2}} \Big( \cos ( \alpha_0 ) \cos ( x) + \sin( \alpha_{0} ) \sin (x) \Big) = \sqrt{a^{2}+b^{2}} \cos ( x - \alpha_{0} ) $)
Essaye d'appliquer, maintenant, cette explication à ton exercice. :happy3:
Pour le deuxième exercice :
Tu poses :
 = e^x - \Big( \displaystyle \sum_{k=0}^n \frac{x^{k}}{k!} \Big) $)
Et tu montres, par récurrence, que
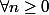
:
 \geq 0 $)
-
MrBrightside
- Membre Naturel
- Messages: 52
- Enregistré le: 05 Sep 2012, 18:12
-
 par MrBrightside » 09 Sep 2012, 17:04
par MrBrightside » 09 Sep 2012, 17:04
Alors le réel que je minore par 0 est:
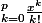
Ce qui fait qu'il me reste:
 \geq \frac{x^{p+1}}{(p+1)!})
C'est mieux là?
@barbu23: Merci mais j'ai déjà résolu mon exercice, mais ta méthode a l'air relativement différente de celle qui m'a été donnée précédemment. Je l'examinerai donc quand j'aurai fini le reste de mon travail. :we:
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 17:12
par Luc » 09 Sep 2012, 17:12
MrBrightside a écrit:Alors le réel que je minore par 0 est:
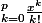
Ce qui fait qu'il me reste:
 \geq \frac{x^{p+1}}{(p+1)!})
C'est mieux là?
Beaucoup mieux. Donc comment conclus-tu?
-
MrBrightside
- Membre Naturel
- Messages: 52
- Enregistré le: 05 Sep 2012, 18:12
-
 par MrBrightside » 09 Sep 2012, 17:17
par MrBrightside » 09 Sep 2012, 17:17
Et bien je fais la limite lorsque x tend vers +l'infini du membre de droite. Puisque p+1! est un réel, je vais trouver que la limite de \frac{x^{p+1}}{p+1!} lorsque x tend vers +infini est +infini. Et par comparaison j'en déduis que le membre de gauche tend également vers +infini.
@barbu23: j'ai vu ton édition, et je te remercie encore simplement pour le fait que tu aies voulu m'aider, malheureusement tu arrives après la bataille si je puis dire. Les questions de mon premier post ont déjà été traitées, et là Luc m'aide à en résoudre une que j'ai posté un peu plus bas. :euh:
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 17:18
par Luc » 09 Sep 2012, 17:18
MrBrightside a écrit:Et bien je fais la limite lorsque x tend vers +l'infini du membre de droite. Puisque p+1! est un réel, je vais trouver que la limite de

lorsque x tend vers +infini est +infini. Et par comparaison j'en déduis que le membre de gauche tend également vers +infini.
C'est correct!
-
MrBrightside
- Membre Naturel
- Messages: 52
- Enregistré le: 05 Sep 2012, 18:12
-
 par MrBrightside » 09 Sep 2012, 17:22
par MrBrightside » 09 Sep 2012, 17:22
Ouf, merci beaucoup. :dodo:
Je vais m'arrêter là pour aujourd'hui, mais demain je reviens à la charge pour finir les exercices de mon DM qui m'ont l'air tout simplement impossible. :ptdr:
Merci à vous 3 pour votre aide précieuse, passez une bonne soirée/nuit et à bientôt. :)
-
mathelot
 par mathelot » 10 Sep 2012, 09:01
par mathelot » 10 Sep 2012, 09:01
bonjour,
l'énoncé de la question 1 est inutilement compliqué. l'enseignant pose l'équation

et attend la réponse suivante dans la copie
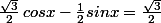
ou la réponse
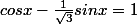
avec
=\frac{1}{\sqrt{3}})
et après, c'est ...fini
cordialement,
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
, on obtient:
, on en déduit donc par comparaison que