Enveloppe d'une famille de droite

[praud]

Comment determiner l'enveloppe de la famille de droite passant par m(1+t;0) et n(0;1-t) pour tout t.

[yos]

Equation de Dt, de D't, et intersection de ces deux droites.

[praud]

pourquoi en determinant l'intersection de d et d' ,on trouve l'enveloppe.L'intersection sera un point?

[alben]

pourquoi en determinant l'intersection de d et d' ,on trouve l'enveloppe.L'intersection sera un point?

Oui, mais il dont les coordonnées dépendront de t et t'. puis seulement de t lorsque t'->t
Ensuite, en faisant varier t, tu as une série de points qui constituent l'enveloppe (une belle conique d'ailleurs)

[praud]

Oui, mais il dont les coordonnées dépendront de t et t'. puis seulement de t lorsque t'->t

Qu' apelle tu t'?

[alben]

Bonsoir,
Excuse moi, je n'ai pas en tête la façon dont les choses sont enseignées aujourd'hui.
Par définition, pour déterminer l'enveloppe d'une famille de courbes dépendant d'un seul paramètre, il faut :
1 calculer l'intersection de deux courbes de la famille, donc avec deux valeurs du paramètre t et t' par exemple
2 rapprocher t' de t et déterminer les ccordonnées du point d'intersection limite
3 On a donc obtenu quelque chose du genre x= f(t) et y = g(t).
C'est l'enveloppe et l'on peut éliminer t pour trouver y=h(x)
Dans le cas très simple ou la famille de courbes est constituée de droite, en posant t'=t+h, on trouve
[INDENT]y = a(t)x +b(t) pour la première et y= a(t+h)x + b(t+h) pour la seconde
l'intersection est donc définie par [(a(t+h)-a(t)]x=b(t)- (b(t+h)
et en passant à la limite lorsque h->0 x = -b'(t)/a'(t)[/INDENT]
Je suppose qu'on vous enseigne ce court-circuit.???
D'une façon comme une autre, on détermine poure chaque t, un point de l'enveloppe et donc finalement l'enveloppe entière.
J'espère avoir clarifié les choses

[yos]

t' est un second paramètre (je le note plutôt s dans ce qui suit).
Dt a pour équation (1-t)x+(1+t)y=1-t²,
Ds a pour équation (1-s)x+(1+s)y=1-s².
Ds et Dt se coupent en de coordonnées ((s+1)(t+1)/2, (1-s)(1-t)/2).
Lorsque s tend vesrs t, le point tend vers de coordonnées ...
La courbe décrite par est l'enveloppe cherchée.
Il faut voir comme le point d'intersection de deux droites infiniment voisines de la famille : 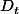et .
Les calculs sont à vérifier.

[yos]

Désolé, vu ta réponse trop tard Alben. Je ne sais pas non plus comment c'est enseigné. Il me semblait que cela n'était plus au programme de prépa, mais comme à la fac ce genre de choses n'a jamais été très prisé, je suppose qu'il s'agit tout de même d'un exo de prépa.

[praud]

on a demontre a une question precedente que si la droite etait donne par des equations cartesienne U(t)*x+v(t)*y+w(t)=0.Determiner l'enveloppe revient a resoudre le systeme (f(t) et g(t) sont les coordonnes du pointM(t)).
U(t)*f(t)+v(t)*g(t)+w(t)=0
U'(t)*f(t)+v'(t)*g(t)+w'(t)=0

[alben]

Bonjour,
Oui, c'est bien l'équivalent de mon "court-circuit" avec des équations de droites non réduites.
Tu trouves bien une parabole inclinée à 45 ° comme enveloppe ?

[praud]

Il faut resoudre le systeme suivant (t-1)*x-y*(1+y)+1-t²=0
x-y-2t=0

[alben]

Il faut resoudre le systeme suivant (t-1)*x-y*(1+y)+1-t²=0
non (t-1)*x-y*(1+t)+1-t²=0
x-y-2t=0

simple erreur de transcription, je présume

[praud]

Je trouve x=((1+t)²)/2,y=((t-1)²)/2.Maintenant je dois demontrer que l'equation cartesienne de l'enveloppe est x²+y²-2xy-4x-4y+4=0.Je dois eliminer le parametre t de quelle facon.

[yos]

En supposant qu'on ne t'ai pas donné le résultat :
calcule x(t)+y(t) et x(t)-y(t) et tu verras plus clair.

[praud]

x(t)+y(t)=((1+2t+t²+t²-2t+1)/2)=(2t²+2)/2=t²+1
x(t)-y(t)=((1+2t+t²-t²+2t-1)/2))=(4t)/2=2t
j'ai pas compris comment ces calculs me permettent d'eliminer t.

[alben]

Tu aurais pu le faire directement à partir du système de ton message de 9h58.
Il suffisait de remplacer t dans la première equation par sa valeur obtenue à partir de la seconde