Enveloppe supérieure de familles de fonctions

[legeniedesalpages]

Bonsoir,

je cherche l'enveloppe supérieure de la famille de fonctions de dans telle que pour tout entier n, \mapsto \sin(2 \pi n x)"/>.

Pour x irrationnel, j'ai trouvé 1.
Mais apparemment ce n'est pas forcément le cas pour les rationnels,
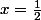
par exemple pour j'ai trouvé 0.

Merci pour votre aide.

[alben]

Bonjour,

Oui, tu as raison. C'est amusant !
On peut montrer avec Bezout que si x=p/q, irréductible, la valeur maxi atteinte par fn(x) sera identique à celle de x=1/q.
Si q est un multiple de 4, f(p/q)=1 sinon f(p/q) <1

[legeniedesalpages]

Bonjour Alben,

merci pour ton aide, je crois que c est exactement ce que je recherche.
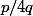
Donc je dois utiliser Bezout pour montrer que les seuls rationnels qui on leur enveloppe sup =1 sont les rationnels du type avec p et q deux entiers premiers entiers.
Je vais tester.

[legeniedesalpages]

hum, en fait j'ai du mal à exploiter bezout,

Alors, je suppose x rationnel.
Si x=0, l'enveloppe sup est 0.

Sinon j'écris x sous forme de fraction irréductible x = p/q.

D'après l'identité de Bezout, il existe deux entiers relatifs u et v tels que
.
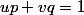
Donc , ie .

Et là je n'arrive pas à exploiter ça pour montrer que la valeur maxi atteinte par fn(x) est identique à celle de x=1/q.

[alben]

oui, on peut même s'arranger pour que u soit positif
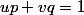
. Donc
et .

[alben]

On aurait aussi pu dire que si x est entier, f(x)=0 et que f(x+k)=f(x) avec k entier

[legeniedesalpages]

D'accord,
mais je ne vois pas comment tu peux imposer u positif, et pourquoi faire?

Ensuite pour x = p/q avec p et q premiers entre eux et q multiple de 4,
je vois bien que l'enveloppe sup est 1.

Par contre, je ne vois pas comment trouver que pour les autres rationnels, ça ne fait pas 1.

[alben]

Bonjour,
Tu peux commencer par remarquer que si x est rationnel, la suite fn(x) est périodique puisque et donc son maxi est atteint. Pour que f(x)=1, il faut donc qu'il existe n tel que
soit encore Comme n,p, k et q sont entiers, cette égalité n'est possible que si q est multiple de 4

[legeniedesalpages]

D'accord tout est clair,
à part juste une notion à éclairer le fait que fn prend un nombre de valeurs finies implique que le sup est un max?

Merci en tout cas pour ton aide, alben qui a été très profitable. :)

[alben]

Oui, dans un ensemble fini totalement ordonné, plus grand élément et borne supérieure sont identiques