Enveloppe convexe !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Juil 2007, 23:36
par barbu23 » 15 Juil 2007, 23:36
Soient :

.
Soit :
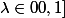
:
alors :
 $)
:

.
 $)
:

.
Il faut montrer que :
.x_{2} \in \overline{S} $)
.
c'est à dire:
.x_{2} ) $)
:

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Juil 2007, 23:45
par barbu23 » 15 Juil 2007, 23:45
ou bien, comme dans le cours, vaut mieux travailler avec les boules au lieu des voisinages :
Soient :

.
Soit :
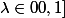
:
alors :

:
 \bigcap S \neq \empty $)
.

:
 \bigcap S \neq \empty $)
.
Il faut montrer que :
.x_{2} \in \overline{S} $)
.
c'est à dire:

:
.x_{2}) \bigcap S \neq \empty $)
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 00:09
par aviateurpilot » 16 Juil 2007, 00:09
kazeriahm a écrit:ok mais on parle bien de combinaisons convees, pas de combinaisons linéaires quelconques
mais moi j'ai utilisé les combinaisons convexes,
essaye de bien relire ma solution, et remarque que la somme des coeifficient que j'ai utilisé egale à 1. donc c'est pas une combinaisons linéaires quelconques. :++:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 00:11
par barbu23 » 16 Juil 2007, 00:11
Soit:

:
On a:

:
 \bigcap S \neq \empty \Longrightarrow \exists z \in S $)
tel que :

:
 \bigcap S \neq \empty \Longrightarrow \exists z' \in S $)
tel que :
.z'-(1-\lambda).x_{2}|| < (1-\lambda).\epsilon $)
(2).

.
.z' -\lambda.x_{1}+(1-\lambda).x_{2}|| \leq ||\lambda.z-\lambda.x_{1}|| + ||(1-\lambda).z'-(1-\lambda).x_{2}|| < \lambda.\epsilon + (1-\lambda).\epsilon = \epsilon $)
.
On pose :
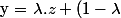.z' \in S $)
car:

est un convexe.
alors:

tel que :
.x_{2}|| < \epsilon $)

.x_{2}) \bigcap S \neq \empty $)
D'où le résultat !!
Est ce qu'il est juste ce raisonnement , et merçi infiniment !!!
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 16 Juil 2007, 00:13
par kazeriahm » 16 Juil 2007, 00:13
oui oui aviateur on est d'accord
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 00:16
par aviateurpilot » 16 Juil 2007, 00:16
barbu23 a écrit:Soient :

.
Soit :
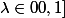
:
alors :
 $)
:

.
 $)
:

.
Il faut montrer que :
.x_{2} \in \overline{S} $)
.
c'est à dire:
.x_{2} ) $)
:

.
là tu veux montrer que
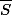
convex.
ta démo est aussi vraie,mais voilà une démo plus simple si tu veux
soit

,
donc
,(y_n))
deux suite de

tel que

converge vers

et

converge vers

.
mtn il est clair que

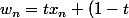y_n\in S)
converge vers
y)
et donc
y\in \overline{S})
car c'est une limite d'une suite
)
de

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 00:20
par barbu23 » 16 Juil 2007, 00:20
Quelqu'un pourrait m'aider à resoudre ce qui suit :
Soit

un convexe tel que: l'interieur de

n'est pas vide.
Montrer que l'adhérence de l'interieur de

est égale à l'adhérence de

..
Pour linclusion directe , c'est évident:
En effet :
L'interieur de

est inclus dans

, donc l'adhérence de l'interieur de

est inclus dans l'adhérence de

..
Maintenant, il reste l'inclusion reciproque..
et merçi d'avance !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 00:22
par barbu23 » 16 Juil 2007, 00:22
Oui absolument, elle est très facile, et sympas ta démo aviateurpilot, merçi !!
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 00:45
par aviateurpilot » 16 Juil 2007, 00:45
c'est quoi la definition de l'interieur d'un ensemble?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 09:51
par barbu23 » 16 Juil 2007, 09:51
On doit vérifier que:

est inclus dans l'adhérence de l'interieur de

:

.
Soit :

:

:
 \bigcap S \neq \empty $)
.
On doit vérifier que :

:
 \bigcap S^{o} \neq \empty $)
.
Est ce que quelqu'un peut m'aider ?!!
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 10:10
par aviateurpilot » 16 Juil 2007, 10:10
c'est quoi la definition de l'interieur, j'ai deja vu les boule et klk notions de topologie en mathsup mais pas la noiton d'interieur,je vais la voir en math spé,
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 16 Juil 2007, 10:18
par kazeriahm » 16 Juil 2007, 10:18
l'intérieur d'un ensemble A c'est
{xA / il existe r>0 vérifiant la boule de centre a et de rayon r est contenue dans A}
c'est le plus grand ouvert contenue dans A
A est ouvert ssi il eswt égal à son intérieur
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 10:25
par barbu23 » 16 Juil 2007, 10:25
L'interieur d'un ensemble

est le plus grand ouvert contenu dans

.
Une partie

de

est ouvert si et seulement si elle est voisinage de chacun de points ... c'est à dire:

.

:
 \subset U $)
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 10:42
par aviateurpilot » 16 Juil 2007, 10:42
merci kazeriahm et barbu23 pour la definition.
tu as deja verifie que

inclus dans
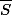
soit

donc
)
une suite de

qui tend vers

soit

et

on pose
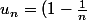x_n+\frac{1}{n}y\in S)
montrons que

)
inclus dans

.
soit G={l'ensemble des segments liant les elements de
)
par

}, mtn il est claire que

(inclus dans

) contien

.
d'ou

.
mtn il est clair que
)
une suite de

qui convrege vers

. donc

d'ou
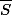
inclus dans
 N.B: j'ai utilisé le fait que
N.B: j'ai utilisé le fait que  est convexe, ce qui est evident
est convexe, ce qui est evident
tu veux que le le montre?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 10:50
par barbu23 » 16 Juil 2007, 10:50
non non c'est clair maintenant, merçi beaucoup aviateurpilot !
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 10:52
par aviateurpilot » 16 Juil 2007, 10:52
barbu23 a écrit:non non c'est clair maintenant, merçi beaucoup aviateurpilot !
de rien,
:++:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 16 Juil 2007, 10:59
par kazeriahm » 16 Juil 2007, 10:59
aviateurpilot a écrit:alors
)
inclus dans

pourquoi ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 12:05
par aviateurpilot » 16 Juil 2007, 12:05
dsl, j'ai oublié la definition d'un ouvert , c'est pour cela que j'ai fait cette faute de logique .lol,
voila une solution:
soit G={l'ensemble des segments liant les element de
)
par

}, mtn il est claire que

(inclus dans

) un ouvert qui contien

.
d'ou

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 14:28
par barbu23 » 16 Juil 2007, 14:28
aviateurpilot, j'ai compris pourquoi :

, mais j'ai pas compris pourquoi

... Tu peux me dire pourquoi ... merçi d'avance !!!
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 15:37
par aviateurpilot » 16 Juil 2007, 15:37
barbu23 a écrit:aviateurpilot, j'ai compris pourquoi :

, mais j'ai pas compris pourquoi

... Tu peux me dire pourquoi ... merçi d'avance !!!
pour voir c'est chose d'une facon bcp plus claire (imaginer).
essaye de construire sur une feuille (plan) une boule de rayon r>0 de centre ( le point y) et un point

est tu va voir la forme de G, (sachant que

est dans le segment

qui coupe G on deux partie symetrique) et tu vien bien remarque que

est a l'interieur de G.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
.
:
:
.
:
.
.
:
.
, mais j'ai pas compris pourquoi
... Tu peux me dire pourquoi ... merçi d'avance !!!