Pour l'ordre, si tu as vérifié que N^{2} et N^{3} ne fait pas l'identité alors oui tu peux dire qu'ellle est d'ordre 4.
Pour le truc c'est un peu subtil faut prendre le temps d'y réfléchir. Ta matrice
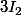
est bien dans
)
. Et son déterminant est non nul, donc en tant que matrice de
)
, elle est inversible. (En fait on utilise un bazooka pour tuer un moustique, on voit tout de suite qu'elle est inversible d'inverse
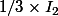
).
Et justement son inverse:
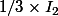
) n'est pas dans
)
.
Reviens à ton ensemble G qui est l'ensemble des matrices de
)
de determinant non nul.
Cette matrice
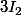
montre bien que G n'est pas stable par passage à l'inverse. (Evidément pour pouvoir parler d'inverse pour la multiplication, il faut bien sur faire remarquer que G est une partie de
)
qui est un groupe, et tu prends son inverse dans cette ensemble.) Donc G ne peut pas etre un groupe pour la multiplication des matrices).
Fait le parralèle avec

et

: 2 est inversible dans

mais son inverse 1/2 n'est pas dans

etc.
