Encadrements délicats

[pouik]

Bonjour,
Je ne comprend un peu rien à ces deux questions don si vous pourriez m'aider ce serait super. Un grand merci à tous ceux qui m'aideront !! :happy2:

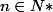
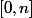
Soit . Donner sans démonstration les variations de sur . n entier
¤ En déduire les valeurs extremes des en fonction de .
J'avoue que je ne vois pas du tout comment faire !!!
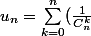¤ Encadrer alors grossièrement, et constater que l'encadrement est insuffisant pour conclure (je pense que c'est sur la limite).
Alors là je vois encore moins !!!! :briques:

[tize]

Bonjour,
As tu repondu à la premiere question ?

[pouik]

bah non parce que je vois pas comment faire pour avoir le snes de variation !!!
On peut calculer la dérivée alors ... hum je sais pas !!!

[tize]

Pour le snes de variation il faut d'abord se syndiquer... :we: (ok c pas drole...)
Sinon il est dit : "sans démonstration..." alors pas besoin de dériver quoi que se soit... tu peux essayer pour quelques valeurs de k (avec n fixé), on voit très vite le max et le min...

[pouik]

bah en fait c'est bizzare parce que :
pour k=0 je trouve 1 : donc je pense que c'est la valeur minimale.
pourk=1 je trouve n : donc je pense que c'est la valeur maximale.
Et enfin je postule qu'à partir du rang 1, cette application est décroissante !!!


Est-ce que c'est ca ou est-ce je que viens de me manger un mur ????? :marteau: :mur:

[yos]

Le triangle de Pascal montre bien les variations de la suite (C(n,k)) pour n fixé.

[pouik]

Bon d'accor je le fais :
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 5 1
...
Mais je ne vois pas comment l'utiliser !!!!

[tize]

Où est la valeur maximale à chaque ligne ?

[pouik]

au centre
et alors là je suit pas bien !!!

[tize]

Bon ba voilà, pour tout n et k, tu connais la valeur minimale et la valeur maximale...

[pouik]

désolé mais alors là je ne comprneds pas du tout !!!

[yos]

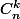
Le plus grand des entiers est donc si n est pair et si n est impair.

[pouik]

et donc les plus petits sont et qui valent tous les deux 1 si j'ai bien comris !!!!

Pour le sens de variation en utilisant le Triangle de Pascal je conjecture que l'application est strictement croissante !!!
est-ce ca ?????

[pouik]

Pouvez-vous me dire si ce que je propose est correct s'il vous plait ???

[yos]

Les plus petits sont et qui valent 1.
Ensuite viennent le second terme et l'avant dernier qui valent n.
Ta somme est donc égale à .
Tous les termes de la somme sont compris entre 0 et 2/[n(n-1)] et il y en a n-3. D'où un encadrement évident de cette somme; sa limite en découle.

[pouik]

donc converge vers 2 alors !!!

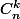
Sinon est bien croissante ???
Et est-ce que si on avait considérer au lieu de la quantité comme tu l'as fait on aurait aboutit ? c'est à dire est-ce qu'on aurait réussi à trouver la limite de la suite ???

merci d'avance. :hein: :hein:

PS : Comment faire pour mettre dans la somme les indices comme tu les mets ?? moi ca fait pas bien !!!

[yos]

donc converge vers 2 alors !!!

Oui.

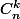
Sinon est bien croissante ???

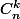
Ben non! Elle croit puis décroit. Dans la ligne n du triangle de Pascal on a les termes de la suite (attention : c'est une suite finie, à moins de considérer les nuls pour k>n). On voit bien le sens de variation.

Et est-ce que si on avait considérer au lieu de la quantité comme tu l'as fait on aurait aboutit ? c'est à dire est-ce qu'on aurait réussi à trouver la limite de la suite ???

C'est pas pour rien que j'ai isolé le second et l'avant-dernier terme de la somme. Essaie autrement et tu verras le problème.

PS : Comment faire pour mettre dans la somme les indices comme tu les mets ?? moi ca fait pas bien !!!

Mets \displaystyle{formule}

[pouik]

MAis pourquoi est-ce que ca n'aboutit pas pour ???

[yos]

Dans cette somme, il y a n-1 termes dont le plus grand est 1/n, ce qui fait que tu peux majorer la somme par (n-1)/n (et la minorer par 0).
Et là tu es chocolat.

[pouik]

merci beacoup pour ton aide j'ai tout compris grâce à toi !!

AU fait je connaossaois pas cette expression "tu es chocolat" : elle est marrante !!!

Bonne fin de soirée !!! :++: :++: