EDP avec Laplacien

par **Aspx** » 25 Juin 2008, 14:52

Bonjour !

Voici mon exercice :
On considère l'équation aux dérivées partielles suivante :

[CENTER]

[/CENTER]

Trouver toutes les fonctions homogène de classe

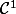
sur

qui vérifient

Bon déjà si

est

-homogène on a forcément

vu la forme de l'équation. Ensuite je pense qu'il faudrait utiliser les coordonnées polaires donc (par abus de notation je note encore

) :
[CENTER]

[/CENTER]

Ensuite je vois vraiment pas comment continuer... Le critère d'Euler me semble par exemple inutile ici :marteau:

par **Aspx** » 25 Juin 2008, 15:13

Je retire ce que j'ai dit, je crois bien qu'il sert énormément (ct logique en mm temps). Ce cher Euler nous dit que
[CENTER]

[/CENTER]

Donc vu (après calcul)

il vient

[CENTER]

[/CENTER]

Reste plus que ce terme avec

à éliminer :mur: (si je ne me trompe pas)

par **Aspx** » 25 Juin 2008, 15:55

Deuxième tentative :

Critère d'Euler + Schwarz =

Donc en remplaçant dans l'équation de base et vu qu'on résout sur

on a
[CENTER]

[/CENTER]

par **Aspx** » 25 Juin 2008, 16:13

J'ai tout refait. J'ai essayé la méthode suivante :
[CENTER]

[/CENTER]
Or je n'aboutis pas à une équation ne faisant intervenir que

et

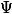
... Pareil en inversant les rôles de

et

pour le choix de

...
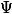
:marteau: :marteau: :marteau: :marteau:

par **Aspx** » 25 Juin 2008, 16:34

4ème tentative et la bonne je crois ! (je me tape un trip solo sur ce thread :we: )

Mix de l'idée précédente avec les coordonnées polaires en plus.

[CENTER]

[/CENTER]

J'obtiens l'équation différentielle suivante :
[CENTER]

[/CENTER]

par **Aspx** » 25 Juin 2008, 16:34

4ème tentative et la bonne je crois ! (je me tape un trip solo sur ce thread :we: )

Mix de l'idée précédente avec les coordonnées polaires en plus.

[CENTER]

[/CENTER]

J'obtiens l'équation différentielle suivante :
[CENTER]

[/CENTER]

Et là je vais tenter de résoudre en cherchant les solutions DSE... Bon pitié venez moi en aide ! :cry: