Droite de régression

[busard_des_roseaux]

Bj,

Soit les coordonnées d'un nuage de points du
plan euclidien.

Peut on chercher une droite de régression d'équation

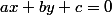
avec les moindres carrés, équation non résolue en la variable y?

Qu'est-ce que ça donne comme formules ?

merci.

[kazeriahm]

bah soit tu cherches un b non nul et la c'est résolu, soit b=0 et la ...

[busard_des_roseaux]

re,

je me lance dans les calculs, on pose:




on cherche à minimiser

on annule les dérivées partielles car il existe un minimum local
sur


les droites de regression(s) passent par le point moyen.

Mais, est-ce que ce déterminant


est nul ? il le faut pour qu'une solution non triviale existe ??

[busard_des_roseaux]

ça marche pas ce que j'ai écrit précédemment

est-ce que je peux minimiser sous la contrainte ?

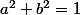
bah soit tu cherches un b non nul et la c'est résolu, soit b=0 et la ...

je voudrais éviter cette discussion..

[kazeriahm]

pourquoi pas ?

Un autre truc qui pourrait être pas mal : on doit avoir a*x+b*y=-c donc il faut trouver (a,b) qui minimise la variance de la statistique (a*x_i+b*y_i)

Une fois qu'on est au minimum en variance, c est donné par la moyenne de cette statistique

Faut regarder ce que ca donne mais a priori ca supprime "un degré de liberté"

[busard_des_roseaux]

pourquoi pas ?

Un autre truc qui pourrait être pas mal : on doit avoir a*x+b*y=-c donc il faut trouver (a,b) qui minimise la variance de la statistique (a*x_i+b*y_i)

je vais regarder sur un exemple.