[Intégrales à paramètre] Domaine d'intégrabilité d'une expon

[Wenneguen]

Bonjour,

je dois déterminer pour quelles valeurs de x la fonction

est définie.
est une fonction continue, positive et de limite égale à en .

J'ai une petite idée sur laquelle j'ai pas mal de doutes :

je sais que la fonction est intégrable sur si et seulement si .
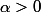
Vu les caractéristiques de , je procède par analogie ce qui me conduit à dire que ma fonction est définie si et seulement si (t-x) t, ce qui n'est pas possible pour tout t puisque t parcourt , et je conclus alors que n'est pas définie.

Qu'en pensez-vous ?

Merci :we:

[Le_chat]

Elle est bizarre ton argumentation, tu peux simplement regarder ce qu'est la limite quand t tend vers l'infini de exp(lambda(t)*(t-x)).

[Wenneguen]

Elle est bizarre ton argumentation, tu peux simplement regarder ce qu'est la limite quand t tend vers l'infini de exp(lambda(t)*(t-x)).

Oui je sentais confusément que je n'allais pas au plus simple ^^

L'intégrande tend vers l'infini en l'infini, donc l'intégrale sur n'est pas définie ! ( j'ai bon ? )

[adrien69]

C'est vrai mais il faut faire gaffe à la justification. Une intégrande qui ne tend pas vers 0 en l'infini peut tout de même être intégrable. Par contre, SI ton intégrande possède une limite en l'infini (que cette limite soit finie ou pas) ET qu'elle est intégrable en l'infini (j'entends par là sur un domaine dont l'extrémité droite est l'infini) ALORS cette limite vaut 0. Ici tu as une limite et elle est non nulle, ce qui contredit l'intégrabilité.

Edit : mais en fait ce n'est pas l'argument le plus simple. Il te suffit de dire que ayant une limite infinie en l'infini, les valeurs prises par cette fonction sont plus grande que 1 à partir d'un certain rang M. Tu conclus alors en minorant ton intégrande pour t plus grand que le maximum de M et de x par une fonction dont l'intégrale diverge. Cette preuve marcherait en fait si avait une limite finie strictement supérieure à 0 à l'infini. Je conclus en te faisant remarquer que je viens presque de donner une preuve du théorème que j'ai employé avant d'éditer mon message

[Wenneguen]

C'est vrai mais il faut faire gaffe à la justification. Une intégrande qui ne tend pas vers 0 en l'infini peut tout de même être intégrable. Par contre, SI ton intégrande possède une limite en l'infini (que cette limite soit finie ou pas) ET qu'elle est intégrable en l'infini (j'entends par là sur un domaine dont l'extrémité droite est l'infini) ALORS cette limite vaut 0. Ici tu as une limite et elle est non nulle, ce qui contredit l'intégrabilité.

Ok je vois merci, l'existence de la limite est décisive. En cours on a vu une fonction en forme de triangles successifs, de hauteurs de plus en plus grandes et de " bases " de moins en moins larges ( ou un truc comme ça ) qui donc n'avait pas le limite en l'infinie et n'était même pas bornée, mais était intégrable sur ]0, + l'infini[ ( et même que l'intégrale faisait pi²/6 :ptdr: )

Je suppose que c'est à ce genre de choses que tu fais référence ? :we:

[adrien69]

Exactement.