Distance projection

[triskaideka]

Bonjour voici mon problème : soit f une fonction de R^2 dans R^k, on connait un K-uplet qui n'a que très peu de chances d'appartenir à l'image de f. Quel distance choisir pour (x, y) tels que trouver f(x,y) le plus proche du K-uplet en question ?
On peut modéliser ça sous forme de K équations à deux inconnues.
Peut être cela vous parait-il un peu flou, et je ne suis pas sur moi-même de comprendre toutes les notions sous-jacentes.
Nous sommes en dimension finie, toutes les normes sont équivalentes, cela veut dire que l'on conserve les inégalités de distance (définie à partir de cette norme) entre les vecteurs. Peut-on dire que peut importe le choix de la norme ?

[miikou]

salut, peut etre peux tu etudier la norme de f(x,y)- (x1, ... xk)
ou (x1,...,xk) est ce 'k-uplet'

[triskaideka]

Oui bien sur, mais mon problème est de bien choisir la norme en question, euclidienne à partir du produit scalaire usuel ? Comme je l'ai dit j'ai l'intuition que cela ne fera pas de différence sur le vecteur qui vérifie le min de cette norme, mais je n'en suis pas vraiment sur, j'ai l'impression que le problème est plus compliqué. Et puis il existe des distances qui ne dérivent pas d'une norme.

[miikou]

tu peux donner lexpression de f stp ?

[triskaideka]

Ah oui j'avais oublié, je fais ça dans un cadre très théorique : en gros f est une fonction dont on ne connait les valeurs qu'en certains points : sur un quadrillage de R^2, j'ai crée une sorte de fonction d'interpolation sur chaque carré de ce quadrillage. Je voulais savoir s'il existe une solution, disons générale, mon prof de maths de l'année dernière nous avait parlé d'un chimiste qui voulait trouver les valeurs de 2 variable dont une fonction dépendait linéairement, il avait 13 équations obtenu grâce à des expériences . Selon lui c'était un problème de projection orthogonale , je ne me souviens plus de sa solution mais il me semble qu'il faudrait un truc dans ce goût là. Désolé de ne pas être plus précis.

[miikou]

je vois pas dsl ...

[legeniedesalpages]

salut,

je pense que pour les normes, on devrait se fixer sur la norme euclidienne pour avoir des "projections orthogonales".

On pourrait peut être construire dans notre cas un exemple de et d'un point de tels que leur distance diffère selon la norme.

(par exemple prendre pour l'équation d'un plan de et un point qui n'est pas dans ce plan et regarder pour ).

Un peu dans le même genre qu'ici: http://www.ilemaths.net/forum-sujet-212618.html

[triskaideka]

Ok , bon je en suis toujours pas sur de tout comprendre à mon problème mais je crois que ça va mieux quand même. On sait que dans un espace euclidien E, la distance d'un vecteur u à un SEV est : inf{||u-v|| / v appartient à ce SEV}, et on sait que le vecteur v tel que ||u-v||=d (la distance) est le projeté orthogonale de u sur ce SEV parrallèlement à son orthogonal. Ce qui me faut en vérité ce serait ce projeté orthogonal. Dans le cadre d'un hyperplan de R^K pas de problème, mais en l'occurence je ne pense pas que Im(f) soit un SEV de R^k (f n'est absolument pas linéaire).
En tout cas merci pour ces réponses.

En y repensant, ne pourrait-t-on pas introduire un plan tangent à f , pour se ramener à cette situation ?

En fait non je suis paumé.

[triskaideka]

Bon je fait un double post, je sais c'est pas bien.
J'ai réfléchi un peu ce week end.
Dans R^k on a un nuage de points (en l'occurence Im(f)), un point est donné par un ses coordonnées dans R^k. On dispose d'un algorithme permettant de trouver le point le plus proche de celui-ci en utilisant une norme particulière.
Peut -on dire que pue importe la norme que l'utilise puisque elles sont toutes equivalentes en dimension finie ?

[busard_des_roseaux]

bonjour,

il est souhaitable de considérer la norme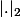 sur car son carré est différentiable et provient du produit scalaire.

soit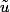 le point de

on trouve le ou les minima du carré de la distance en annulant la différentielle
de


d'où deux inconnues et et deux égalités dans




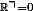
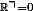
où les crochets sont le produit scalaire habituel.

[triskaideka]

D'accord, merci pour cette réponse, l'avantage n'est donc que dans la méthode de calcul pour cette norme au carré (qui était celle que je voulais utiliser).
J'aimerais savoir si mon raisonnement est juste, en partant du fait que toutes les normes sont équivalentes en dimension finis ( il existe deux réels c et C strictement positifs tels que quel que soit x appartenant à E, c*N1(x)<=N2(x)<=C*N2(x)), on prouve facilement que si N1(x)<=N1(y) alors N2(x)<=N2(y), et là je ne sais pas si je peux conclure ou non, que peut importe la norme choisi le point le plus proche sera toujours le même.

[busard_des_roseaux]

que peut importe la norme choisi le point le plus proche sera toujours le même.

et bien non, comme on change de norme, ça revient à minimiser des fonctions différentes.

[triskaideka]

Oui mais cela les empêche -t-elle d'avoir leur minimum atteint au même point ?
Concrètement je ne vois pas où est mon erreur.
Ensuite si il y a des différences que peut-on savoir des solutions (x,y) qui nous seront données par l'algorithme en fonction de la norme choisie?
Merci.

Non parceque je ne suis pas rester sans rien faire, j'ai pris un exemple sans doute très simple, mais bon : Dans R^3 on cherche le point du plan d'equation : z=x+y le plus proche du poin (1,1,1). Pour trois normes (1,2 et 4)j'ai trouvé le même minimum. Je me suis aidé de graphe pour vérifier que malgré d'autres points critiques, il n'y avait qu'un seul minimum. Je ne sais pas trop comment mener mes calculs pour la norme infini, mais peut être n'ai-je pas tout faut. C'est d'ailleurs ce que m'avait conseillé le génie des alpages.