bonjour,
voila je bloque sur un exo
soit f la fonction suivante : f(x,y) = ln( 1 + x*exp(y) ) - y²x si x > 0
ln( 1 + x*exp(y) ) sinon
question : quelle est le dl a l'ordre 2 en ( 0 , 0 ) ? on traira avec soin la questions des petit o
on a que ln ( 1 + x*exp(y) ) -y²x = x*exp(y) - x²exp(2y)/2 + o( x²exp(2y) ) - y²x
maintenant le dl de exp nous donne : x( 1+y+o(y) ) - x²(1 + 2y +o(y) )/2 - y²x + o( x²exp(2y) ) = x + xy - x²/2 - x²y - x²*o(y)/2 - y²x + o( x²exp(2y) ) + x*o(y)
maintenant je doit montré que -x²y - x²*o(y)/2 - y²x + o( x²exp(2y) ) + x*o(y) = o( x²+y²) et c'est la où je bloque
Développement limité
3 messages
- Page 1 sur 1
Re: développement limité
Bonjour
Une façon simple pour montrer que chaque terme) c'est d'utiliser la norme 2.
c'est d'utiliser la norme 2.
||_2^2=x^2+y^2=r^2) (en passant en coordonnées polaires)
(en passant en coordonnées polaires)
Par exemple)^2 r sin(t)|\leq r^3)
d'où=o(x^2+y^2)...)
Et par ailleurs chaque monôme de degré 3 est un o(x^2+y^2)
autre exemple=o(x^2+y^2)) .
.
En effety=\epsilon(x,y)) où
où ) tend vers 0 quand (x,y) tend vers 0.
tend vers 0 quand (x,y) tend vers 0.
Donc=xy \epsilon (x,y) = r^2 cos(t) sin(t)\epsilon(x,y)) ensuite passer à la valeur absolue et majoration par
ensuite passer à la valeur absolue et majoration par 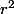 fois une fonction qui tend vers 0.
fois une fonction qui tend vers 0.
Si j'ai bien compris on te demande de revenir aux définitions pour bien justifier (comprendre) que dans chaque cas que tu as bien un)
Une façon simple pour montrer que chaque terme
Par exemple
d'où
Et par ailleurs chaque monôme de degré 3 est un o(x^2+y^2)
autre exemple
En effet
Donc
Si j'ai bien compris on te demande de revenir aux définitions pour bien justifier (comprendre) que dans chaque cas que tu as bien un
Re: développement limité
Bonjour,
à ce sujet, je me demandais si, au delà de la formule de Taylor Young à 2 variables, il existait une théorie un peu rigoureuse des développements limités à deux variables... aviateur, tu connais ?
à ce sujet, je me demandais si, au delà de la formule de Taylor Young à 2 variables, il existait une théorie un peu rigoureuse des développements limités à deux variables... aviateur, tu connais ?
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
