Développement limité (sup)

[Plimpton]

Bonjour !

Mon prof de maths un peu fou nous a donné ce weekend un exercice vraiment long : donner le DL 4 en x=0 de f(x)=tan(x+pi/4) ^ -cotan(2x)
(désolé, je ne maitrise pas encore votre outil merveilleux qui sert à écrire de belles formules ^^)
Je suis bloqué vers la fin.
Mon idée était de mettre la fonction sous forme exponentielle :
f(x)=exp(-cotan(2x)*ln(tan(x+pi/4)))
Autrement dit :
f(x)=exp(-cotan(2x)*ln((1+tan(x))/(1-tan(x))))

À partir de la, j'ai trouvé :
f(x)=exp(-1+(2/3)x^2+(26/45)x^4+o(x^4))
C'est ici que je bloque. f ne tend pas vers e^0 quand x tend vers l'infini, donc il faudrait faire un changement de variable ? Comment feriez-vous ?

Merci !

[pascal16]

un DL en 0 est par définition très proche de la fonction en 0, mais s'en écarte de plus en plus grand on s'écarte de 0.
Or +oo est très loin de 0

[Plimpton]

Bonsoir. Evidemment, mais je pensais justement faire un changement de variable avec un variable qui tendrait vers 0 et non pas 1

J'ai fait une erreur dans ma phrase plus haut, je voulais dire "f ne tend pas vers e^0 quand x tend vers 0"

[Ben314]

Salut,

J'ai fait une erreur dans ma phrase plus haut, je voulais dire "f ne tend pas vers e^0 quand x tend vers 0"

Déjà, ça n'a rien d'étonnant vu que, si tu regarde la formule de départ, lorsque x->0, le truc "sous" l'exposant tend vers 1 alors que l'exposant tend vers +oo donc c'est une forme indéterminée et on sait pas trop d'avance quelle va être la limite, et il y est parfaitement plausible que ce soit exp(-1).

Ensuite, ben tu t'en fout un peu de savoir vers quoi tend f(x) pour calculer ton D.L.
Arrivé à ce point, si tu t'es pas gouré, tu as du exp(???) avec ??? qui tend vers -1 (lorsque x tend vers 0) et il faut un peu réfléchir pour voir comment procéder (il y a au moins deux solutions).

[Ben314]

Sinon, perso., j'aurais décomposé le truc en deux temps en écrivant que
avec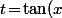
(même calcul préliminaire que toi plus tan(2t)=... et ln(A/B)=ln(A)-ln(B))
Et j'aurais sans doute commencé par déterminer le D.L. en pour en déduire celui en avec juste une hésitation concernant le fait de savoir si le passage t->x je le fait avant ou après l'exponentielle, mais le truc dans l'exponentielle, je l'aurais clairement fait entièrement en d'abord.