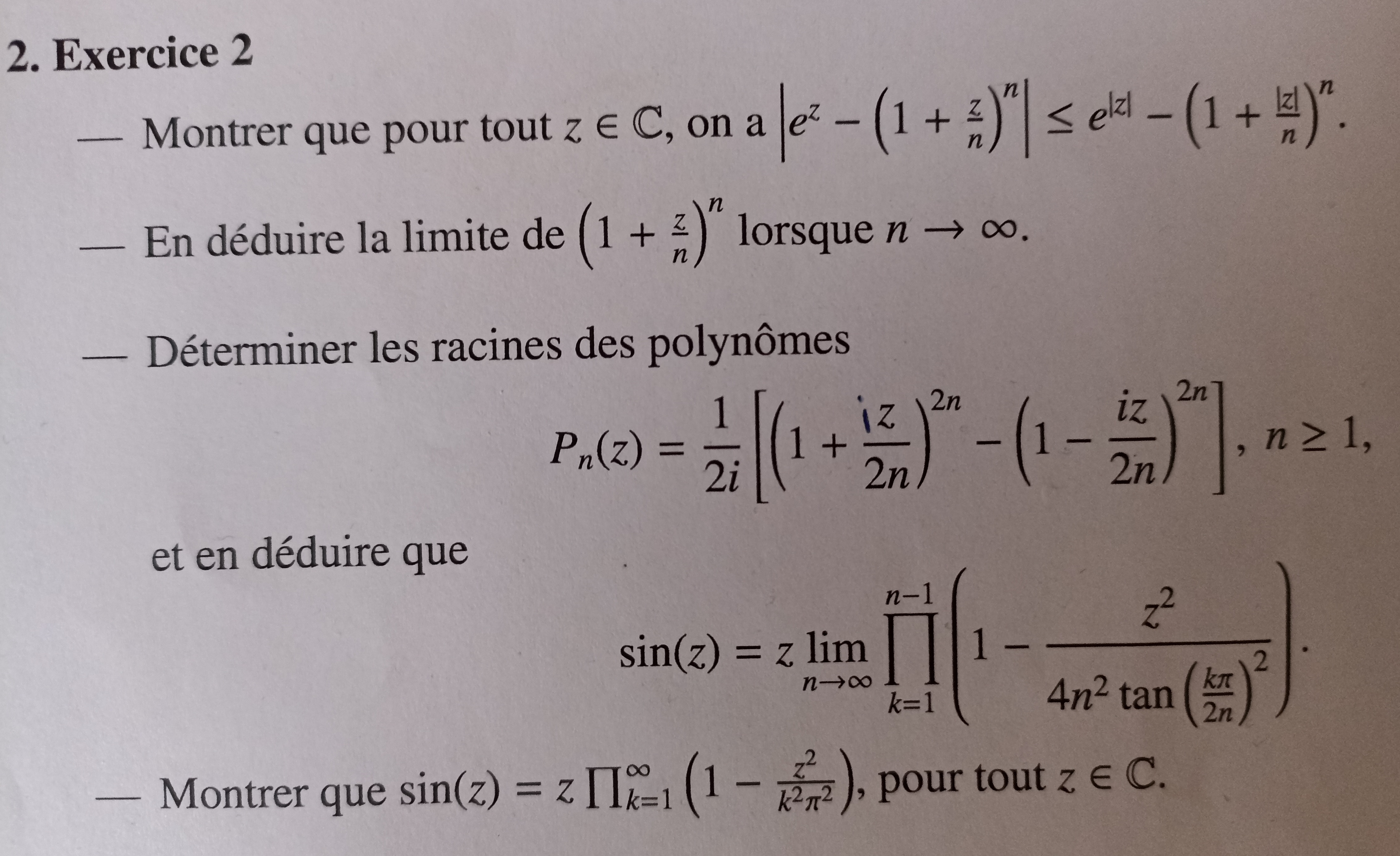Bonjour à tous, je sèche sur certaines questions d'un exercice où l'on prouve une formule du développement du sinus en produits infinis due à Euler :
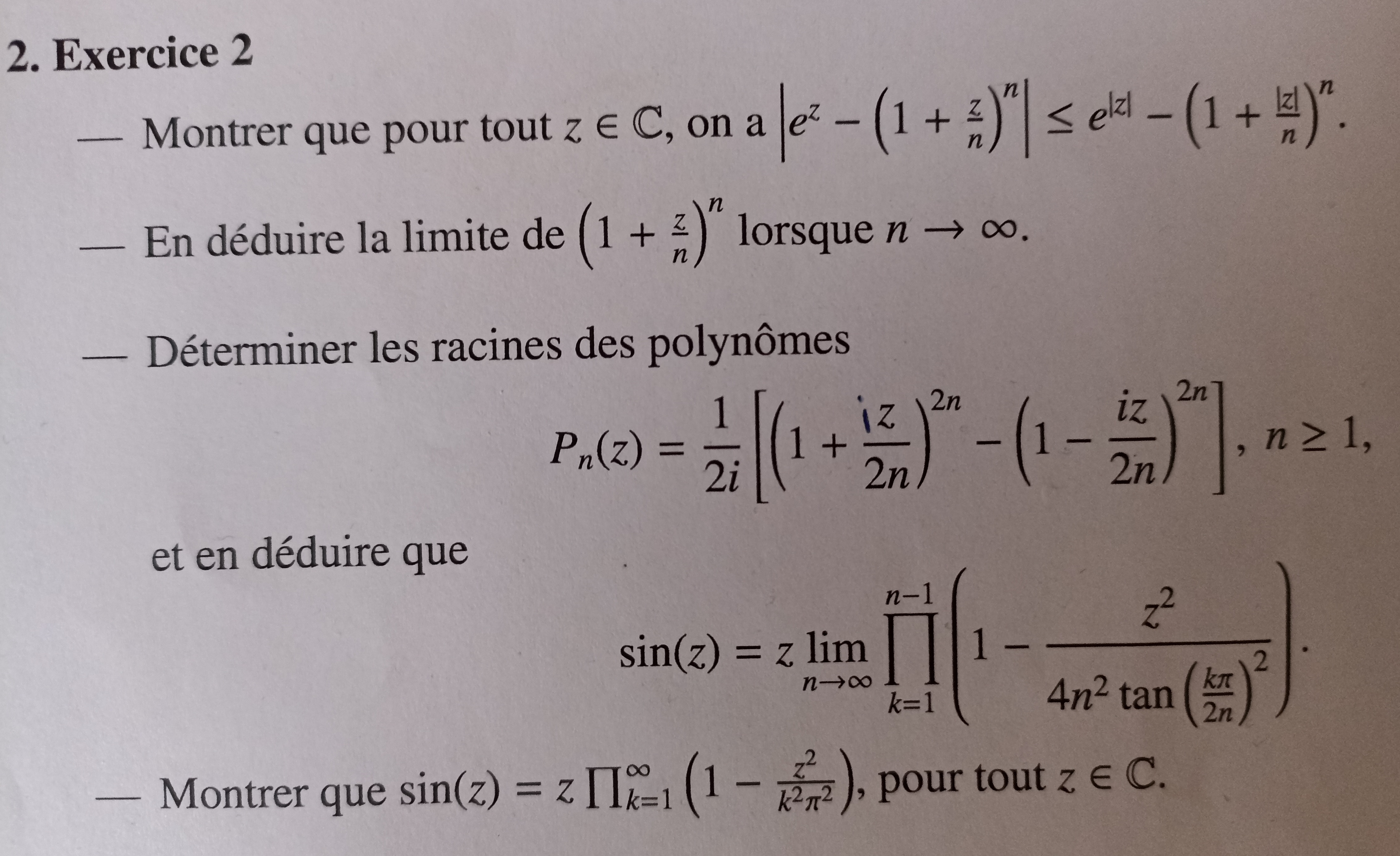
(1) Je sèche dès la première question.
Je montre déjà que pour tout
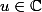
, on a déjà
| \le e^{|u|} - (1+ |u|}))
. En effet,
| = |\sum_{n=2}^{+ \infty} \frac{u^n}{n!}| \le \sum_{n=2}^{+ \infty} \frac{|u|^n}{n!} = e^{|u|} - (1+ |u|))
.
Maintenant, pour tout

, on a par la formule de factorisation dans les anneaux :
^n = (e^u - (1+u)) \sum_{k=0}^{n-1}(e^{ku})(1+u)^{n-k-1})
c'est à dire :
^n| \le |e^u - (1+u)| \sum_{k=0}^{n-1} |e^u|^k |1+u|^{n-k-1})
Or,

et

d'où

ce qui nous donne :
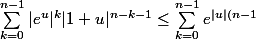} = n e^{|u|(n-1)})
Et là ça me plaît pas trop, l'idéal serait de majorer la somme par
})
et on aurait alors, puisque
} \le (1 + |u|)^{n-1})
le résultat suivant :
^n| \le |e^u - (1+u)| \, e^{|u|(n-1)} \le e^{|u|} - (1+ |u|) e^{|u|(n-1)} \le e^{n|u|} - (1+|u|)(1+|u|)^{n-1} = e^{n|u|} - (1+|u|)^n)
.
Enfin, en prenant

on aurait le résultat annoncé mais hélas... on a ce

qui traîne..
La (2) s'en déduit immédiatement puisque
^n = e^{|z|})
on en déduit que
^n| = 0)
donc que
^n = e^z)
pour tout
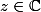
.
(3)J'ai
 = 0 \Longleftrightarrow (1 + \frac{iz}{2n})^{2n} = (1 - \frac{iz}{2n})^{2n})
c'est à dire, pour tout

:
 = 0 \Longleftrightarrow (\frac{1+\frac{iz}{2n}}{1-\frac{iz}{2n}})^{2n} = 1 \Longleftrightarrow \frac{1+\frac{iz}{2n}}{1-\frac{iz}{2n}} = e^{\frac{2ik \pi}{2n}} = e^{\frac{ik \pi}{n}})
pour

d'où :
 = 0 \Longleftrightarrow 2n + iz = (2n - iz)e^{\frac{ik \pi}{n}} \Longleftrightarrow iz(1 + e^{\frac{ik \pi}{n}}) = 2n (e^{\frac{ik \pi}{n}} - 1) \Longleftrightarrow z = 2in \frac{1- e^{\frac{ik \pi}{n}}} {1 + e^{\frac{ik \pi}{n}}} = 2n \tan(\frac{k \pi}{2n}))
en factorisant par l'angle moitié.
Mais attention cette écriture avec la tangente n'est pas valable si
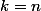
car
)
n'est pas définie. Si
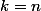
on a
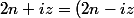e^{\frac{in \pi}{n}} = -1)
soit

et cette équation n'a pas de solution en

Du coup j'ai envie de dire que les racines du polynôme c'est tous les
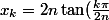)
pour

et

, donc
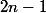
racines, ce qui est cohérent car le polynôme

est en réalité de degré
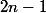
(les coefficients en

se télescopent)
(4) On remarque que
 = \sin(z))
d'après la question (2)
D'après la question précédente

s'écrit
 = C_n \prod_{\substack{0 \le k \le 2n-1 \\ k \ne n}} (z - 2n\tan(\frac{k \pi}{2n})))
.
En factorisant le premier terme
 = z - 0)
et en remarquant que les
)
sont symétriques par rapport à l'axe imaginaire dans le demi-cercle trigo supérieur, on a pour
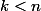
:
 \pi}{2n}) = - \tan(\frac{k \pi}{2n}))
et donc :
 = \displaystyle\lim_{n \to \infty} C_n z \prod_{k=1}^{n-1}(z-2n\tan(\frac{k \pi}{2n}))(z+2n\tan(\frac{k \pi}{2n})) = \displaystyle\lim_{n \to \infty} C_n z \prod_{k=1}^{n-1}(z^2-4n^2\tan^2(\frac{k \pi}{2n})))
Ensuite, je n'arrive pas à calculer

. Si jamais il valait

, il y aurait encore un souci par rapport à la formule attendue vu qu'eux ils ont
)
au dénominateur. Bref je ne comprends pas comment on y parvient
(5) Puisque

un développement asymptotique de
)
est
^2)
, ce qui fournit la formule demandée après multiplication des DL.
Toute aide est la bienvenue. Merci d 'avance