Determination de fonction

[Anonyme]

comment trouver une fonction qui verifie f(0)=0 et que pour tout t appartenant a un intervalle (a determiner) que [f(t)]²=f(t)-t et quelle sont ces dervive 1 et 2.

[boulay59]

Tu as quoi comme hypothèses sur f : est-elle continue, dérivable, C², ou rien de tout ???

[Anonyme]

f est derivable .J'ai meme calcule plusieurs valeur de f.

f(-2)=2
f(-6)=3
f(-12)=4
f(-20)=5
f(-30)=6
f(-42)=7
f(-56)=8
f(-72)=9
f(-90)=10

[danskala]

salut,

on a donc f(t) est solution de

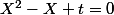
On exprime

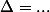
bye

[Anonyme]

j'ai pas compris ce que tu as fait.

[danskala]

[f(t)]²=f(t)-t est équivalent à [f(t)]²-f(t)+t=0

donc f(t) est solution de l'équation X²-X+t=0 d'inconnue X.

X²-X+t est un polynôme du 2nd degré.
On exprime son discriminant

Et ensuite, on discute suivant le signe de ce discriminant pour savoir dans quels cas X²-X+t=0 a au moins une solution.

[Anonyme]

1-4*t est positif si t est inferieur a -1/4 ,null pour pour t=-1/4 ,et negatif pour t superieur -1/4..
L'equation admet deux solution si t<-1/4 et une si t=-1/4.