Dernière question d'un exo-transformation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 24 Oct 2012, 16:41
par wserdx » 24 Oct 2012, 16:41
Ton premier calcul c'est
})
, donc ton calcul final c'est bien
)
Ensuite je ne vois pas bien où tu bloques.
On a déterminé qu'on devait avoir
 = z + \vec{v}/2 = z + (\alpha +1)/2)
qui est une translation.
Ensuite on doit avoir
 = \alpha \bar{z} + i\lambda\sqrt{\alpha})
qui est la symétrie qu'on cherche (pour l'instant seul

(réel) est inconnu)
Peut tu vérifier à partir de ces hypothèses que
 = \alpha \bar{z} + i\lambda\sqrt{\alpha} + (\alpha +1)/2)
?
Il ne reste plus qu'à trouver

pour que la relation

soit vraie,
soit : trouve

tel que pour tout

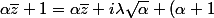/2)
aide :

-
LL54
 par LL54 » 24 Oct 2012, 17:42
par LL54 » 24 Oct 2012, 17:42
[CENTER]tout est supprimée[/CENTER]
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 24 Oct 2012, 18:00
par wserdx » 24 Oct 2012, 18:00

: c'est la translation de
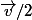
: c'est dans ton énoncé.
la symétrie

admet pour axe

Si je lui ajoute une translation dans la direction orthogonale (c'est-à-dire selon l'axe

) j'obtiens une symétrie dont l'axe est parallèle.
donc
 = \alpha\bar{z} +i\lambda \sqrt{\alpha})
, lorsque

décrit l'ensemble des réels, c'est toutes les symétries d'axes parallèles à la symétrie

-
LL54
 par LL54 » 24 Oct 2012, 18:05
par LL54 » 24 Oct 2012, 18:05
[CENTER]tout est supprimée[/CENTER]
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 24 Oct 2012, 18:20
par wserdx » 24 Oct 2012, 18:20
LL54 a écrit:Ahh je comprend un peu mieux, Merci
Mais comment on sait que elle admet pour axe

?
0 et

sont points fixes:

-
LL54
 par LL54 » 24 Oct 2012, 18:22
par LL54 » 24 Oct 2012, 18:22
[CENTER]tout est supprimée[/CENTER]
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 24 Oct 2012, 18:25
par wserdx » 24 Oct 2012, 18:25
Des points fixes de la symétrie

Tu m'as demandé comment trouver l'axe de cette symétrie. Je t'en ai donné ses points fixes.
-
LL54
 par LL54 » 24 Oct 2012, 18:30
par LL54 » 24 Oct 2012, 18:30
[CENTER]tout est supprimée[/CENTER]
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités