Dérivé de racine(x*y)

[Nico128]

Hello!

Je cherchais la déviré racine(x*y) en fonction de x. Je me suis dit :
racine(x*y) = racine(x) * racine(y)
dérivé : racine(y) / (2 * racine(x))

Pourtant la réponse c'est :
dérivé : y / (2 * racine(x*y))

Pourquoi je ne peux extraire la racine(x*y) en racine(x) * racine(y) ?

Merci

[Anneauprincipal]

Il n'y a pas de problèmes :

[Anonyme]

@Nico128

si tu cherches à dériver racine(x*y) en fonction de x

ET SI y ne dépend pas de x alors comme racine(x*y)=racine(x)*racine(y)

dans le calcul de la fonction dérivée : le nombre racine(y) se comporte comme une constante
et on a :

racine'(x*y)=racine(y)*racine'(x)

et comme racine'(x)=1/(2*racine(x))

on obtient racine'(x*y)=racine(y)/(2*racine(x))

[Nico128]

Il n'y a pas de problèmes :

Haaaaaaaaaaaaaa!!!! Effectivement ^^ J'étais pas au courant.

Merci!

[Anonyme]

@Nico128

Peux tu expliquer car moi , désolé , mais je n'ai pas compris en quoi cette formule permet
de calculer la fonction dérivée de le fonction f définie par

merci

[chan79]

Il n'y a pas de problèmes :

attention cette formule est fausse si y est négatif
la dérivée est cependant toujours si y n'est pas nul

[Anneauprincipal]

@Ptitnoir

C'est juste qu'il n'a pas vu que les deux formules à priori différentes (sa réponse et celle attendue) sont en fait les mêmes. Évidemment que l'on considère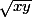 directement ou que l'on sorte le 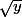avant de faire le calcul ne change rien.

Le ne dépend à priori évidemment pas de , et bien sûr cette formule n'est applicable que là où elle a du sens (donc ). Si et sont tous les deux négatifs, alors avec on obtient donc la dérivée par rapport à x est .