Dénombrement - le retour :-)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
par Anonyme » 28 Aoû 2005, 07:44
Bonjour,
Suite au topic fermé
http://maths-forum.com/showthread.php?t=4757ne laissons pas la grossièreté des uns nuire à la beauté des mathématiques !
Généralisons l'énoncé, et proposons une solution.
Soit S(n,m) le nombre de n-uplets
)
d'entiers naturels compris entre 0 et m tels que
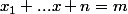
Alors :
=\({m+n-1\\m}\)=\({m+n-1\\n-1}\)})
Lemmeinspiré de
http://www.ilemaths.net/forum-sujet-43630.html=\Bigsum_{k=1}^m (\({n+k\\n}\)-\({n-1+k\\n}\)) + \({n-1\\n-1}\)=\({n+m\\n}\)-\({n\\n}\)+\({n-1\\n-1}\)= \({n+m\\n}\))
=\({n+m\\n}\)=\({n+m\\m}\)})
n=1Avec un nombre, il n'y a qu'une seule façon d'atteindre m :
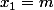
=1})
n=2
peut varier entre 0 et m
doit alors être égal à
=m+1})
n=3 peut varier entre 0 et m
et
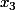
vérifient alors
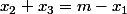
=\Bigsum_{x_1=0}^m S(2,m-x_1)=\Bigsum_{x_1=0}^mm-x_1+1=\Bigsum_{k=0}^{m+1}k=\frac{(m+1)(m+2)}{2}=\({m+2\\2}\))
=\({m+2\\2}\)})
Vérifions pour m=n=3
0 0 3
0 1 2
0 2 1
0 3 0
1 0 2
1 1 1
1 2 0
2 0 1
2 1 0
3 0 0
=> 10 cas et
)
n=4De même :
=\Bigsum_{x_1=0}^m \({m-x_1+2\\2}\)=\Bigsum_{k=0}^m \({2+k\\k}\)=\({m+3\\3}\))
en utilisant le lemme
=\({m+3\\3}\)})
Vérifions pour m=2 et n=4
0 0 0 2
0 0 2 0
0 2 0 0
0 1 0 1
0 1 1 0
0 0 1 1
1 1 0 0
1 0 1 0
1 0 0 1
2 0 0 0
=> 10 cas et
)
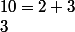D'où la
conjecture :
=\({m+n-1\\m}\)=\({m+n-1\\n-1}\))
DémonstrationOn procède par récurrence sur n.
La propriété est vraie pour n=1, 2, 3 et 4
Supposons
Avec le même raisonnement que dans les exemples ci-dessus, et en utilisant le lemme :
=\Bigsum_{x_1=0}^mS(n,m-x_1)=\Bigsum_{k=0^}^mS(n,k)=\Bigsum_{k=0}^m\({k+n-1\\n-1}\)=\({m+n\\n}\))
CQFD
Sauf erreur.
Nicolas
-
sept-épées
- Membre Naturel
- Messages: 90
- Enregistré le: 24 Aoû 2005, 14:24
-
par sept-épées » 28 Aoû 2005, 11:00
Dieu, que les maths sont belles ! merci pour cette généralisation vertigineuse...
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
par Alpha » 28 Aoû 2005, 11:59
Je tiens à te féliciter, Nicolas, c'est remarquable, en effet!
Ce que j'avais fait était aussi juste, mais jusquà un certain point. En fait, je n'aurais pas du diviser par
, comme phenomene me l'a expliqué par mp, mais la formule que j'avais avant de diviser par
était juste, et est équivalente à celle qui vient d'être démontrée (et qui était celle de phenomene).
Cordialement
-
Anonyme
par Anonyme » 28 Aoû 2005, 12:42
Merci, Alpha !
-
sept-épées
- Membre Naturel
- Messages: 90
- Enregistré le: 24 Aoû 2005, 14:24
-
par sept-épées » 28 Aoû 2005, 13:02
si l'ironie a la vie dure, c'est parce qu'elle a le bonheur de n'être pas toujours comprise... :ptdr:
-
Anonyme
par Anonyme » 28 Aoû 2005, 13:03
Une propriété proche, qui sera utile pour résoudre le problème situé ici :
http://maths-forum.com/showthread.php?p=24072Soit
)
le nombre de n-uplets
)
d'entiers naturels
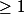
(c'est la nouveauté) tels que
.
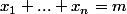
Alors :
=\({m-1\\n-1}\))
n=1 doit valoir m :
=1})
n=2 peut valoir 1, ... m-1 (pour laisser de la place à
)
Puis
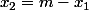
=m-1})
n=3 peut valoir 1, ..., m-2 (pour laisser de la place à
et
)
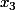
Puis
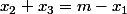
=\Bigsum_{x_1=1}^{m-2}m-1-x_1=\Bigsum_{k=1}^{m-2}k=\frac{(m-1)(m-2)}{2})
=\({m-1\\2}\))
On
conjecture que
DémonstrationLa propriété est vraie pour n=1, 2 et 3.
Supposons la relation vraie au rang n.
Que vaut T(n+1,m) ?
peut varier entre 1 et m-n (pour laisser de la place à
, ...,
)
Et
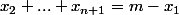
Donc :
=\Bigsum_{x_1=1}^{m-n} \({m-x_1-1\\n-1}\)=\Bigsum_{k=0}^{m-n-1} \({n-1+k\\n-1}\)=\({n+m-n-1\\n}\)=\({m-1\\n}\))
CQFD
La suite ici :
http://maths-forum.com/showthread.php?p=24072Nicolas
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
par Galt » 28 Aoû 2005, 13:10
Si on n'autorise pas la valeur 0 pour les
n entiers, il y a une solution géométrique à ce problème : on cherche à planter
n-1 piquets aux points d'abscisse entière sur l'intervalle [0 ;
m ] (en excluant les extrêmités). Il y a
)
possibilités.
Si on autorise la valeur 0, ça se complique car les piquets peuvent être plusieurs à la même place. Peut-on retrouver la formule précédente par ce genre de raisonnement ?
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
par Alpha » 28 Aoû 2005, 13:10
Sept-épées, je trouve que l'effort de recherche et de rédaction de Nicolas_75 était à saluer, et donc je ne vois pas où peut se trouver l'ironie.
Cordialement.
-
Anonyme
par Anonyme » 28 Aoû 2005, 13:20
Galt, merci pour ta démonstration alternative du second problème, bien plus rapide et élégante !
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
par Galt » 28 Aoû 2005, 14:04
J'ai une idée pour le problème avec la valeur 0 autorisée.
Dans le cas où on se limite aux entiers strictement positifs, on voit qu'il est équivalent de chercher
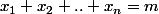
ou
(les
représentant les piquets). Dans le cas ou les
peuvent être nuls, les inégalités précédentes deviennent des inégalités larges
, et on peut les transformer en inégalités strictes en posant
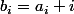
, on a alors
, ce qui redonne bien le résultat
)
-
Anonyme
par Anonyme » 28 Aoû 2005, 14:11
Bien vu ! Bravo.
-
Anonyme
par Anonyme » 28 Aoû 2005, 14:59
Voici une
3ème démonstration du premier problème (où les 0 sont autorisés), en utilisant l'idée des piquets de
Galt.
Soit z le nombre de "0" dans le n-uplet.
On plante les n-z-1 piquets restants :
)
possibilités
On choisit où on met les "0" dans le n-uplet :
)
possibilités
Donc :
=\Bigsum_{z=0}^{n-1}\({n\\z}\)\({m-1\\n-z-1}\))
\({m-1\\k}\))
Or
 X^i=(1+X)^{n+m-1}=(1+X)^n(1+X)^{m-1})
X^j \Bigsum_{l=0}^{m-1}\({m-1\\l}\)X^l)
\({m-1\\k}\))X^i)
En identifiant les termes en
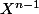
, il vient :
\({m-1\\k}\)=\({n+m-1\\n-1}\))
Donc :
=\({n+m-1\\n-1}\))
Nicolas
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
