barbu23 a écrit:Le problème est comment on fait pour trouver ce

pédagogiquement, quand on commence à étudier la continuité des fonctions en

avec des epsilons et des étas, on donne aux
apprentis-analystes des fonctions de classe C1 qui sont donc localement lipschitziennes.
Alors,

vaut

où le max de f ' est pris sur un voisinage quelconque compact de

. On a donc le choix !!!
et on obtient l'inégalité finale en appliquant une majoration issue du thm des accroissements finis.
-f(x_{0})| \leq (max_{K}|f'|) \times |x-x_{0}|)
Noter aussi que les epsilons et les étas sont utilisés dans les espaces métriques et qu'il y a une définition plus générale de la continuité
avec des ouverts appartenant à une topologie.
Exemple: pour montrer la continuité de la fonction "carré"
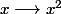
en
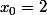
on prend arbitrairement le voisinage compact K=[1;3] de

la dérivée

y est majorée en valeur absolue
par 6 et l'on obtient:
si
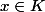
alors

cordialement.
