Démonstration d'inégalité
40 messages
- Page 1 sur 2 - 1, 2
Démonstration d'inégalité
Bonsoir à tous,
Je suis actuellement en prépa ECE et je suis face à un petit problème, le voici :
En considérant le trinôme suivant : P(x)=(a1x+b1)^2+(a2x+b2)^2+(a3x+b3)^2, en sachant que a1,a2,a3,b1,b2,b3 sont des réels quelconques et que donc les 1,2,3 sont des indices.
Je dois montrer que : (a1b1+a2b2+a3b3)^2<=(a1^2+a2^2+a3^2)(b1^2+b2^2+b3^2)
J'ai essayé en développant tout d'abord dans les deux sens, ceci n'a rien donné.
Donc j'ai tenté de travailler avec le discriminant du polynôme dans lequel je m'y suis perdu.
Je ne vous demande pas de me le faire en entier, il n'y aurait aucun intérêt mais juste un petit début comme une indication pour que j'avance dans ma démonstration.
Merci d'avoir lu ce message et à bientôt j'espère =)
Je suis actuellement en prépa ECE et je suis face à un petit problème, le voici :
En considérant le trinôme suivant : P(x)=(a1x+b1)^2+(a2x+b2)^2+(a3x+b3)^2, en sachant que a1,a2,a3,b1,b2,b3 sont des réels quelconques et que donc les 1,2,3 sont des indices.
Je dois montrer que : (a1b1+a2b2+a3b3)^2<=(a1^2+a2^2+a3^2)(b1^2+b2^2+b3^2)
J'ai essayé en développant tout d'abord dans les deux sens, ceci n'a rien donné.
Donc j'ai tenté de travailler avec le discriminant du polynôme dans lequel je m'y suis perdu.
Je ne vous demande pas de me le faire en entier, il n'y aurait aucun intérêt mais juste un petit début comme une indication pour que j'avance dans ma démonstration.
Merci d'avoir lu ce message et à bientôt j'espère =)
Arony a écrit:Je suis d'accord avec toi mais en quoi ceci me permet de me démontrer ceci.
c'est ce pont là que je ne comprends pas
Premièrement, en développant
Écris le sous la forme
D'autre part,
Arony a écrit:Du coup, de manière analogue , je suis arrivé à l'inégalité de cauchy-schwartz.
Comment a partir de cette inégalité, je peux déduire des minorations ou majorations ?
Merci d'avance !
Il y a plein dinégalités qui sont des applications de Cauchy-Schwarz (Sans t celui ci, contrairement à Laurent Schwartz qui est un autre mathématicien, du XXè siècle celui-là).
Une façon de voir Cauchy-Schwarz est de dire que la valeur absolue du produit scalaire est inférieure au produit des normes. Donc dès que tu as un produit scalaire sur un espace vectoriel, tu peux appliquer Cauchy-Schwarz et hopefully en déduire des inégalités intéressantes. Rien n'interdit de choisir des espaces vectoriels exotiques comme des espaces de fonctions, etc.
Hop, je reposte l'équation 
Pour le produit scalaire, tu n'as pas vu le produit scalaire de deux vecteurs du plan en première S?
Cela suffit largement pour comprendre cette interprétation de Cauchy-Schwarz.
La pour pouvoir appliquer Cauchy-Schwarz on a envie de dire que et
et
 sont des normes. (pour pouvoir minorer le produit, par Cauchy-Schwarz). Quel serait le "produit scalaire" correspondant?
sont des normes. (pour pouvoir minorer le produit, par Cauchy-Schwarz). Quel serait le "produit scalaire" correspondant?
PS : Si tu ne vois pas, tu peux toujours prendre n=2 et essayer de voir quelle minoration tu peux établir directement (avec des arguments du type : identité remarquable + un carré est toujours positif)
Pour le produit scalaire, tu n'as pas vu le produit scalaire de deux vecteurs du plan en première S?
Cela suffit largement pour comprendre cette interprétation de Cauchy-Schwarz.
La pour pouvoir appliquer Cauchy-Schwarz on a envie de dire que
PS : Si tu ne vois pas, tu peux toujours prendre n=2 et essayer de voir quelle minoration tu peux établir directement (avec des arguments du type : identité remarquable + un carré est toujours positif)
Bon en fait, il y a un moyen direct un peu astucieux de minorer cette quantité. En effet,
(\sum_{k=1}^{n} \frac{1}{x^k})=\sum_{k=1}^{n} \sum_{l=1}^{n}x^{k-l}) =
= (termes en
(termes en 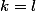 ) +
) + }{2}) termes de la forme
termes de la forme  avec
avec  .
.
On utilise ensuite la minoration bien connue (en tout cas très utile) .
.
Et on obtient(\sum_{k=1}^{n} \frac{1}{x^k}) \geq n+2\frac{n(n-1)}{2} \geq n+n(n-1)=n^2) .
.
Tu peux essayer de te demander si le cas d'égalité est possible en cherchant un exemple de x pour lequel ce cas est atteint.
On utilise ensuite la minoration bien connue (en tout cas très utile)
Et on obtient
Tu peux essayer de te demander si le cas d'égalité est possible en cherchant un exemple de x pour lequel ce cas est atteint.
Non On ne l'a pas vu.
C'est un exercice, je tente de prendre de l'avance sur les TD.
On devait partir du polynôme que j'ai posé plus haut, et nous en sommes arrivé à cette inégalité.
Puis, maintenant je dois "surment à apprendre à l'appliquer" donc, il me demander de prouver une minoration de ce que j'ai posé et par la suite, y a une majoration à identifier.
Donc je pense qu'on a fait indirectement la démonstration tout le long et maintenant, je dois l'appliquer deux fois : Une fois pour la minoration ( Le problème posé ici) et une majoration d'une autre somme.
C'est un exercice, je tente de prendre de l'avance sur les TD.
On devait partir du polynôme que j'ai posé plus haut, et nous en sommes arrivé à cette inégalité.
Puis, maintenant je dois "surment à apprendre à l'appliquer" donc, il me demander de prouver une minoration de ce que j'ai posé et par la suite, y a une majoration à identifier.
Donc je pense qu'on a fait indirectement la démonstration tout le long et maintenant, je dois l'appliquer deux fois : Une fois pour la minoration ( Le problème posé ici) et une majoration d'une autre somme.
Arony a écrit:Salut, Luc, j'ai su retrouver ton raisonnement du coup, il y a la minoration dans ton développement si j'ai bien compris.
Avec les valeurs absolus, il aurait fallu faire comment ? ça sera toujours un plus pour moi si je le sais le jour des concours.
En te remerciant d'avance =)
Et bien ici, on travaillait avec des nombres réels positifs, donc pas besoin de valeur absolue.
Lorsque tu travailles avec les valeurs absolues, il n'y a que deux inégalités à connaître et à utiliser :
1)
2) L'inégalité triangulaire
Remarque que cette inégalité triangulaire implique que
(au moins un des deux nombres |x|-|y| et |y|-|x| étant négatif, il n'y a qu'une des deux inégalités qui est intéressante).
L'inégalité triangulaire peut également se généraliser par récurrence à n nombre réels, et même aux nombres complexes.
40 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
