salut!
J'ai un petit DM a faire et j'avoue que j'ai un peu de mal à démarrer.
Voilà l'énoncé:
on sait que la constante d'euler notons la y=lim n-->+infini (somme pour k allant de 1 à n de (1/k) - ln(n) )
( c'est apparement connu mais je vous la rapelle quand même :hein: )
Démontrer que:
somme pour n allant de 1 à +infini de ( (-1)^n *ln/n ) = yln2 - 0.5(ln2)²
Voilà je vous remercie d'avance si vous trouvez ne serait ce qu'une méthode ou si vous pouvez m'aider à débuter
et je vous remercie encore plus si vous pouvez le démontrer
a+
Démonstration avec constante d'euler
8 messages
- Page 1 sur 1
Très joli et plutôt inattendu :++:
Déjà ça converge car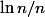 est décroissante pour n > 3.
est décroissante pour n > 3.
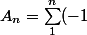^k \ln{k}/k)
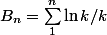
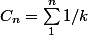
C'est très très pénible à écrire, juste les grandes lignes :
- Par des manips simples on obtient que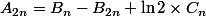
- En comparant avec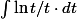 ,
, }^2/2)
-}^2/2 - B_n =) ... (en créant une somme télescopique) ...
... (en créant une somme télescopique) ... 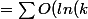/k^2)) convergente i.e
convergente i.e 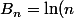}^2/2 + cste + o(1))
La conclusion suit en regroupant tout ce bazard.
Déjà ça converge car
C'est très très pénible à écrire, juste les grandes lignes :
- Par des manips simples on obtient que
- En comparant avec
-
La conclusion suit en regroupant tout ce bazard.
Quelques précision
Merci ThSQ pour avoir répondu parceque comme l'a remarqué Aeripz ma formule était plutot dure à lire...
Donc vraiment merci
Je dis bravo pour les feintes mais j'ai un problème pour démontrer la première formule que tu obtient par "des manips simples" . Je suppose qu'il faut cuisiner les suites. J'imagine que ca doit être chiant à écrire mais pourrait tu quand même m'en dire un peu plus
Et est-ce que calculer A(2n) revient en + infini à calculer A(n) ??
Merci
a+
Donc vraiment merci
Je dis bravo pour les feintes mais j'ai un problème pour démontrer la première formule que tu obtient par "des manips simples" . Je suppose qu'il faut cuisiner les suites. J'imagine que ca doit être chiant à écrire mais pourrait tu quand même m'en dire un peu plus
Et est-ce que calculer A(2n) revient en + infini à calculer A(n) ??
Merci
a+
Si (An) a une limite, alors (A2n) a aussi une limite, qui est la même, comme suite extraite de (An).
Je n'ai pas regardé de quoi il était question... Mais si tu cherches la limite de (An), et que tu sais qu'elle admet une limite ( en gros, tu sais qu'elle converge, sinon, c'est immédiat... ) alors tu peux chercher la limite de (A2n), qui sera la même !
J'éspère avoir été assez clair ^^
Je n'ai pas regardé de quoi il était question... Mais si tu cherches la limite de (An), et que tu sais qu'elle admet une limite ( en gros, tu sais qu'elle converge, sinon, c'est immédiat... ) alors tu peux chercher la limite de (A2n), qui sera la même !
J'éspère avoir été assez clair ^^
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
