Constante d'Euler
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Sep 2018, 11:24
par mehdi-128 » 10 Sep 2018, 11:24
Bonjour,
On a :
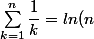 + \gamma + o(1))
Je comprends pas comment on obtient :
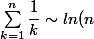)
Je voulais utiliser que :
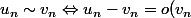)
Mais je n'arrive pas ici...
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 10 Sep 2018, 11:42
par Pseuda » 10 Sep 2018, 11:42
Bonjour,
C'est pourtant immédiat : une constante et une suite qui tend vers 0, sont négligeables devant une suite qui tend vers l'infini, donc la somme des 2 aussi.
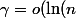))
et
=o(\ln( n)))
.
On a bien le résultat cherché.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Sep 2018, 14:09
par mehdi-128 » 10 Sep 2018, 14:09
J'ai pas compris ça veut dire quoi :
=o(ln(n)))
Dans le cours on a :
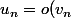)
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 10 Sep 2018, 14:18
par pascal16 » 10 Sep 2018, 14:18
les égalité se lisent de droite à gauche, on utilise = alors que ce n'est pas symétrique.
o(1)=o(ln(n))
se lit " une chose négligeable devant une constante est encore plus négligeable devant ln(n)"
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Sep 2018, 14:50
par mehdi-128 » 10 Sep 2018, 14:50
J'ai toujours pas compris :
Dans le cours :
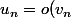 \Leftrightarrow \lim\limits_{n \rightarrow +\infty} \dfrac{u_n}{v_n} =0)
 = o( ln(n)) \Leftrightarrow ...)
Comment appliquer la définition ici j'ai 2 petits o ?
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 10 Sep 2018, 15:13
par pascal16 » 10 Sep 2018, 15:13
quand on écrit o(n), c'est que des termes non écrits sont négligeables devant n
o(1)=o(ln(n))
se lit de gauche à droite
j'ai des termes non écrits négligeables devant 1
ce termes sont donc négligeables devant ln(n)
car
(mes termes non écrits) / 1 -> 0
=> (mes termes non écrits) / ln(n) -> 0
et on voit que c'est une implication, pas une équivalence.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Sep 2018, 15:17
par mehdi-128 » 10 Sep 2018, 15:17
pascal16 a écrit:quand on écrit o(n), c'est que des termes non écrits sont négligeables devant n
o(1)=o(ln(n))
se lit de gauche à droite
j'ai des termes non écrits négligeables devant 1
ce termes sont donc négligeables devant ln(n)
car
(mes termes non écrits) / 1 -> 0
=> (mes termes non écrits) / ln(n) -> 0
et on voit que c'est une implication, pas une équivalence.
Merci j'ai compris
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Sep 2018, 15:33
par mehdi-128 » 10 Sep 2018, 15:33
Merci pour vos réponses Pascal et Pseuda j'ai enfin compris :
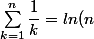 + \gamma + o(1))
Or :
 = o(ln(n)))
et
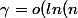))
Donc :
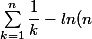 = 2 \times o (ln(n)) = o(2ln(n)) = o (ln(n)))
D'où l'équivalent.

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 10 Sep 2018, 15:40
par Sake » 10 Sep 2018, 15:40
Salut Mehdi-128,
o(1) ça veut dire "petit devant 1", et plus rigoureusement que c'est asymptotiquement négligeable devant 1. Cela veut dire que si une suite (u) est telle que u_n = o(1), alors la limite en l'infini de u_n/1 vaut 0, donc c'est une suite qui tend vers 0. On comprend que toute suite qui tend vers 0 a un terme général qui devient APCR très petit devant le terme général d'une suite qui diverge. Ici, la limite en l'infini de 1/ln(n) est 0, donc o(1) = o(ln(n))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Sep 2018, 16:20
par mehdi-128 » 10 Sep 2018, 16:20
Ah d'accord une suite qui tend vers 0 est négligeable devant une suite qui tend vers l'infini
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 10 Sep 2018, 20:56
par Pseuda » 10 Sep 2018, 20:56
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Sep 2018, 22:33
par mehdi-128 » 10 Sep 2018, 22:33
Oui mais je crains que je suis en train de tout mélanger entre petit o grand O équivalent

Va falloir que je m'entraine sur des exos.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 11 Sep 2018, 09:50
par Pseuda » 11 Sep 2018, 09:50
C'est le même principe pour les o et les O.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
